For the circle ax2+y2+bx+dy+2=0 centre is (1,2) then 2b+3d=
−16
16
8
−8
The correct Answer is:A
To solve the problem, we need to find the values of b and d from the given equation of the circle and then calculate 2b+3d.
1. Identify the standard form of the circle equation:
The general equation of a circle is given by:
ax2+y2+bx+dy+2=0
We can compare this with the standard form:
x2+y2+2gx+2fy+c=0
From this comparison, we can identify that a=1, g=b2, and f=d2.
2. Use the center of the circle:
The center of the circle is given as (1,2). From the center coordinates, we have:
h=−gandk=−f
Therefore, we can write:
1=−b2and2=−d2
3. Solve for b and d:
From the first equation:
1=−b2⟹b=−2
From the second equation:
2=−d2⟹d=−4
4. Calculate 2b+3d:
Now substitute the values of b and d into the expression 2b+3d:
2b+3d=2(−2)+3(−4)=−4−12=−16
5. Final answer:
Therefore, the value of 2b+3d is:
−16
The general equation of a circle is given by:
ax2+y2+bx+dy+2=0
We can compare this with the standard form:
x2+y2+2gx+2fy+c=0
From this comparison, we can identify that a=1, g=b2, and f=d2.
The center of the circle is given as (1,2). From the center coordinates, we have:
h=−gandk=−f
Therefore, we can write:
1=−b2and2=−d2
From the first equation:
1=−b2⟹b=−2
From the second equation:
2=−d2⟹d=−4
Now substitute the values of b and d into the expression 2b+3d:
2b+3d=2(−2)+3(−4)=−4−12=−16
Therefore, the value of 2b+3d is:
−16
Similar Questions
Find the value of a if
2x2+ay2−2x+2y−1=0 represents a circle and also find its radius.
(ii) Find the values of a,b if
ax2+bxy+3y2−5x+2y−3=0 represents a circle. Also find the radius and centre of the circle.
(iii) If x2+y2+2gx+2fy=0 represents a circle with centre (-4,-3) then find g,f and the radius of the circle.
(iv) If the circle x2+y2+ax+by−12=0 has the centre at (2,3) then find a ,b and the raidus of the circle.
(v) If the circle x2+y2−5x+6y−a=0 has radius 4 , find a
View SolutionFind the equation of a circle which passes the centre of the circle x2+y2−6x=1 and concentric with the circle 2x2+2y2−8x+12y−1=0.
View SolutionLet A be the centre of the circle x2+y2−2x−4y−20=0. If the tangents at the points B (1, 7) and D(4,−2) on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
View SolutionThe radius of the circle ax2+(2a−3)y2−4x−7=0 is : (A) 1 (B) 53 (C) 43 (D) 3
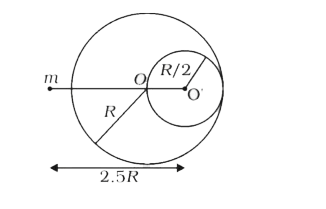
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
View SolutionIf the roots of ax2+bx+c=0 are 2, 32 then (a+b+c)2
View SolutionCoordinates of the centre of the circle which bisects the circumferences of the circles x2+y2=1;x2+y2+2x−3=0 and x2+y2+2y−3=0 is
View SolutionIf two distinct chords drawn from the point (a,b) on the circle x2+y2−ax−by=0 (where ab≠0) are bisected by the x-axis, then the roots of the quadratic equation bx2−ax+2b=0 are necessarily. (A) imaginary (B) real and equal (C) real and unequal (D) rational
View SolutionIf the straight line ax+by=2;a,b≠0, touches the circle x2+y2−2x=3 and is normal to the circle x2+y2−4y=6, then the values of 'a' and 'b' are ?
View SolutionConsider the circle x2+y2=1 and thhe parabola y=ax2−b(a>0). This circle and parabola intersect at
View Solution
