If (mi,1/mi),i=1,2,3,4 are concyclic points, then the value of m1m2m3m4 is
1
−1
0
∞
The correct Answer is:A
To solve the problem, we need to determine the value of m1m2m3m4 given that the points (mi,1mi) for i=1,2,3,4 are concyclic.
1. Understanding the Points: The points given are (m1,1m1),(m2,1m2),(m3,1m3),(m4,1m4). These points lie on a circle, meaning they satisfy the equation of a circle.
2. Equation of the Circle: The general equation of a circle can be written as:
x2+y2+2gx+2fy+c=0
where g,f,c are constants.
3. Substituting the Points into the Circle's Equation: For each point (mi,1mi), we substitute x=mi and y=1mi into the circle's equation:
m2i+(1mi)2+2gmi+2f(1mi)+c=0
4. Multiplying Through by m2i: To eliminate the fraction, multiply the entire equation by m2i:
m4i+1+2gm3i+2fmi+cm2i=0
5. Rearranging the Equation: Rearranging gives us:
m4i+2gm3i+cm2i+2fmi+1=0
6. Forming a Polynomial: This is a polynomial of degree 4 in m with roots m1,m2,m3,m4.
7. Using Vieta's Formulas: According to Vieta's formulas, the product of the roots of a polynomial ax4+bx3+cx2+dx+e=0 is given by:
Product of roots=ea
Here, a=1 (coefficient of m4) and e=1 (constant term).
8. Calculating the Product: Therefore, we have:
m1m2m3m4=11=1
Final Answer:
The value of m1m2m3m4 is 1.
x2+y2+2gx+2fy+c=0
where g,f,c are constants.
m2i+(1mi)2+2gmi+2f(1mi)+c=0
m4i+1+2gm3i+2fmi+cm2i=0
m4i+2gm3i+cm2i+2fmi+1=0
Product of roots=ea
Here, a=1 (coefficient of m4) and e=1 (constant term).
m1m2m3m4=11=1
The value of m1m2m3m4 is 1.
Similar Questions
If (mi,1mi),i=1,2,3,4 are concyclic points then the value of m1m2m3m4 is
View SolutionIf (mi,1mi),mi>0,i=1,2,3,4 are four distinct points on a circle, show that m1m2m3m4=1.
View SolutionIf (mi,1mi),i=1,2,3,4 are four distinct points on a circle, show that m1m2m3m4=1
View SolutionIf m1andm2 are slopes of the tangents to the ellipse x216+y29=1 which passes through (5, 4), then the value of (m1+m2)−(m1m2) is equal to
View SolutionIf (1+i1−i)m=1,then find the least integral value of m.
View Solution(i) Find the value of 'a' if the lines 3x−2y+8=0, 2x+y+3=0 and ax+3y+11=0 are concurrent.
(ii) If the lines y=m1x+c1, y=m2x+c2 and y=m3x+c3 meet at point then shown that :
c1(m2−m3)+c2(m3−m1)+c3(m1−m2)=0
View SolutionThe value of ∞∑m=1tan−1(2mm4+m2+2) is
View Solutiontwo tangents of a hyperbola x2a2−y2b2=1 having m1m2 cuts the axes at 4 concyclic points .find value of m1 m2
View SolutionIf the value of m4+1m4=119 then the value of ∣∣∣m3−1m3∣∣∣=
View SolutionIn the given diagram , find the relation between acceleration of blocks m1andm2 . (m2 remains horizontal ).
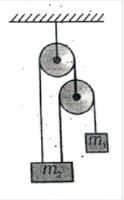
View Solution
