If I1,I2,I3 are the intercept on x-axis, y-axis, y=x w.r.t x2+y2−14x−10y+24=0 then
I2>I3>I1
I3>I1>I2
I1>I3>I2
I3>I2>I1
The correct Answer is:B
To solve the problem, we need to find the intercepts I1,I2,I3 of the circle given by the equation x2+y2−14x−10y+24=0 on the x-axis, y-axis, and the line y=x respectively.
Step 1: Rewrite the Circle Equation
First, we rewrite the given equation of the circle in a more standard form by completing the square.
The equation is:
x2+y2−14x−10y+24=0
Completing the square for x and y:
- For x:
x2−14x=(x−7)2−49
- For y:
y2−10y=(y−5)2−25
Substituting back into the equation:
(x−7)2−49+(y−5)2−25+24=0
(x−7)2+(y−5)2−50=0
(x−7)2+(y−5)2=50
This represents a circle with center (7,5) and radius √50.
Step 2: Find the x-intercept I1
To find the x-intercept, set y=0:
(x−7)2+(0−5)2=50
(x−7)2+25=50
(x−7)2=25
Taking the square root:
x−7=5orx−7=−5
Thus, x=12 or x=2.
The x-intercepts are 12 and 2. Therefore, the length of the x-intercept I1 is:
I1=12−2=10
Step 3: Find the y-intercept I2
To find the y-intercept, set x=0:
(0−7)2+(y−5)2=50
49+(y−5)2=50
(y−5)2=1
Taking the square root:
y−5=1ory−5=−1
Thus, y=6 or y=4.
The y-intercepts are 6 and 4. Therefore, the length of the y-intercept I2 is:
I2=6−4=2
Step 4: Find the intercept I3 on the line y=x
Substituting y=x into the circle's equation:
(x−7)2+(x−5)2=50
Expanding:
(x−7)2+(x−5)2=(x2−14x+49)+(x2−10x+25)=50
Combining like terms:
2x2−24x+74=50
2x2−24x+24=0
Dividing by 2:
x2−12x+12=0
Using the quadratic formula:
x=−b±√b2−4ac2a=12±√144−482=12±√962=6±4√6
The intercepts are 6+4√6 and 6−4√6.
Thus, the length of the intercept I3 is:
I3=(6+4√6)−(6−4√6)=8√6
Step 5: Compare I1,I2,I3
Now we have:
- I1=10
- I2=2
- I3=8√6
Calculating 8√6:
√6≈2.45⇒8√6≈19.6
Thus, we find:
I3>I1>I2⇒8√6>10>2
Conclusion
The correct order of the intercepts is:
I3>I1>I2
First, we rewrite the given equation of the circle in a more standard form by completing the square.
x2+y2−14x−10y+24=0
- For x:
x2−14x=(x−7)2−49
- For y:
y2−10y=(y−5)2−25
(x−7)2−49+(y−5)2−25+24=0
(x−7)2+(y−5)2−50=0
(x−7)2+(y−5)2=50
To find the x-intercept, set y=0:
(x−7)2+(0−5)2=50
(x−7)2+25=50
(x−7)2=25
Taking the square root:
x−7=5orx−7=−5
Thus, x=12 or x=2.
I1=12−2=10
To find the y-intercept, set x=0:
(0−7)2+(y−5)2=50
49+(y−5)2=50
(y−5)2=1
Taking the square root:
y−5=1ory−5=−1
Thus, y=6 or y=4.
I2=6−4=2
Substituting y=x into the circle's equation:
(x−7)2+(x−5)2=50
Expanding:
(x−7)2+(x−5)2=(x2−14x+49)+(x2−10x+25)=50
Combining like terms:
2x2−24x+74=50
2x2−24x+24=0
Dividing by 2:
x2−12x+12=0
Using the quadratic formula:
x=−b±√b2−4ac2a=12±√144−482=12±√962=6±4√6
The intercepts are 6+4√6 and 6−4√6.
I3=(6+4√6)−(6−4√6)=8√6
Now we have:
- I1=10
- I2=2
- I3=8√6
√6≈2.45⇒8√6≈19.6
I3>I1>I2⇒8√6>10>2
The correct order of the intercepts is:
I3>I1>I2
Similar Questions
x2+y2−14x−10y+24=0 makes an
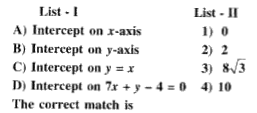
View Solutionx2+y2−14x−10y+24=0 makes an
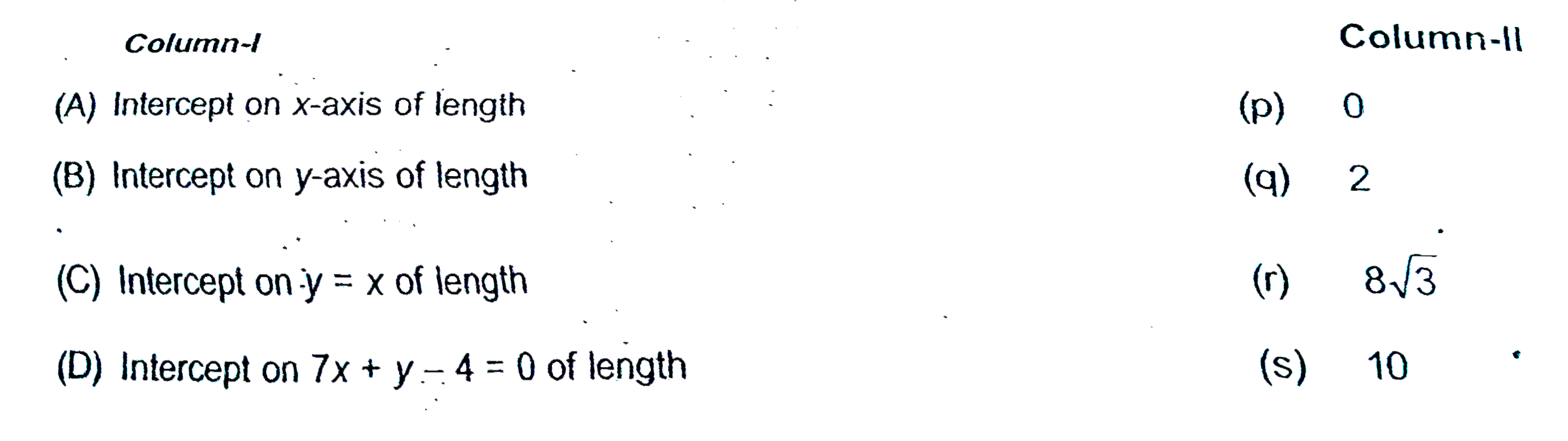
View SolutionIf the points (k,1) (2,-3) are conjugate w.r.t. x2+y2+4x−6y−12=0 then k
View SolutionThe midpoint of the chord 3x−y=10 w.r.t x2+y2=18 is
View SolutionShow that the equation of the circles touching the Y-axis at (0,3) and making an intercept of 8 units on X-axis are x2+y2−10x−6y+9=0
View SolutionThe mid point of the chord x−2y+7=0 w.r.t the circle x2+y2−2x−10y+1=0 is
View SolutionThe intercept made by the circle x2+y2+4x−8y+c=0 on x-axis is 2√10 then c=
View SolutionIf kx+3y=1,2x+y+5=0 are conjugate liens w.r.t the circle x2+y2−2x−4y−4=0 then k=
View SolutionLocate the position of the point (2,4) w.r.t the circle x2+y2−5x−6y+11=0
View SolutionThe chord of contact of (3,-1) w.r.t the circle x2+y2+2x−4y+1=0 is
View Solution
