Given that ΔABC∼ΔDEF,BC=3cm,EF=4cm ans the area of ΔABC is 54sq.cm.Then find the area of ΔDEF.
The correct Answer is:C
To find the area of triangle DEF given that triangle ABC is similar to triangle DEF, we can follow these steps:
Step 1: Understand the relationship between the triangles
Since triangles ABC and DEF are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
Step 2: Write down the given values
- Length of side BC in triangle ABC = 3 cm
- Length of side EF in triangle DEF = 4 cm
- Area of triangle ABC = 54 sq. cm
Step 3: Set up the ratio of the sides
The ratio of the sides BC and EF is:
BCEF=34
Step 4: Set up the ratio of the areas
Since the triangles are similar, the ratio of their areas is given by:
Area of △ABCArea of △DEF=(BCEF)2
Substituting the known values:
54Area of △DEF=(34)2
Step 5: Calculate the square of the ratio of the sides
Calculating (34)2:
(34)2=916
Step 6: Set up the equation
Now we can set up the equation:
54Area of △DEF=916
Step 7: Cross-multiply to solve for the area of triangle DEF
Cross-multiplying gives us:
54⋅16=9⋅Area of △DEF
Calculating 54⋅16:
54⋅16=864
So,
864=9⋅Area of △DEF
Step 8: Solve for the area of triangle DEF
Now divide both sides by 9:
Area of △DEF=8649=96 sq. cm
Final Answer
The area of triangle DEF is 96 sq. cm.
---
Since triangles ABC and DEF are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
- Length of side BC in triangle ABC = 3 cm
- Length of side EF in triangle DEF = 4 cm
- Area of triangle ABC = 54 sq. cm
The ratio of the sides BC and EF is:
BCEF=34
Since the triangles are similar, the ratio of their areas is given by:
Area of △ABCArea of △DEF=(BCEF)2
Substituting the known values:
54Area of △DEF=(34)2
Calculating (34)2:
(34)2=916
Now we can set up the equation:
54Area of △DEF=916
Cross-multiplying gives us:
54⋅16=9⋅Area of △DEF
Calculating 54⋅16:
54⋅16=864
So,
864=9⋅Area of △DEF
Now divide both sides by 9:
Area of △DEF=8649=96 sq. cm
The area of triangle DEF is 96 sq. cm.
Similar Questions
The side of a square is 4 cm. Find its area.
View SolutionABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
View SolutionIn ΔABC,AB=AC=x,BC=10cm and the area of triangle is 60 cm2. Find x.
View SolutionΔABC is isosceles with AB=AC=7cm and BC=9cm. The height AD from A to BC, is 6cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
View SolutionIn the given figure , ∠1=∠2and∠3=∠4. If BC= 7.5 cm , DE= 12.5cm and area of △ABC=13.5cm2 . Find the area of △ADE.

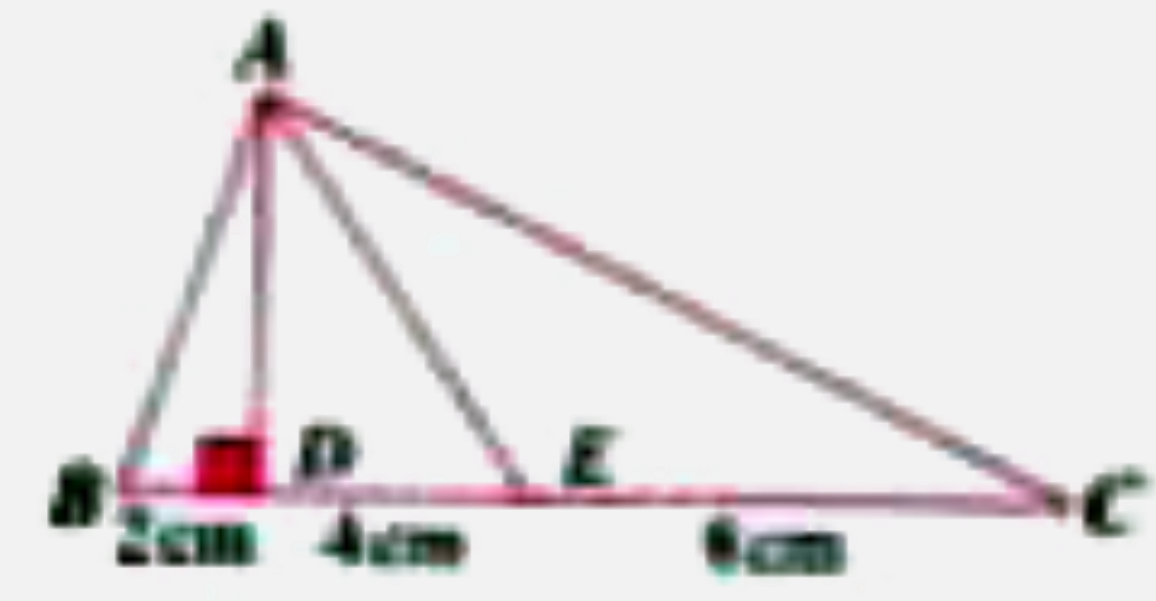
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View SolutionLMNO is a parallelogram where OP is perpenducular to AB. If OM=20cm,LP=9cm, and area of ΔLPO=54sq.cm, find the perimeter of LMNO.
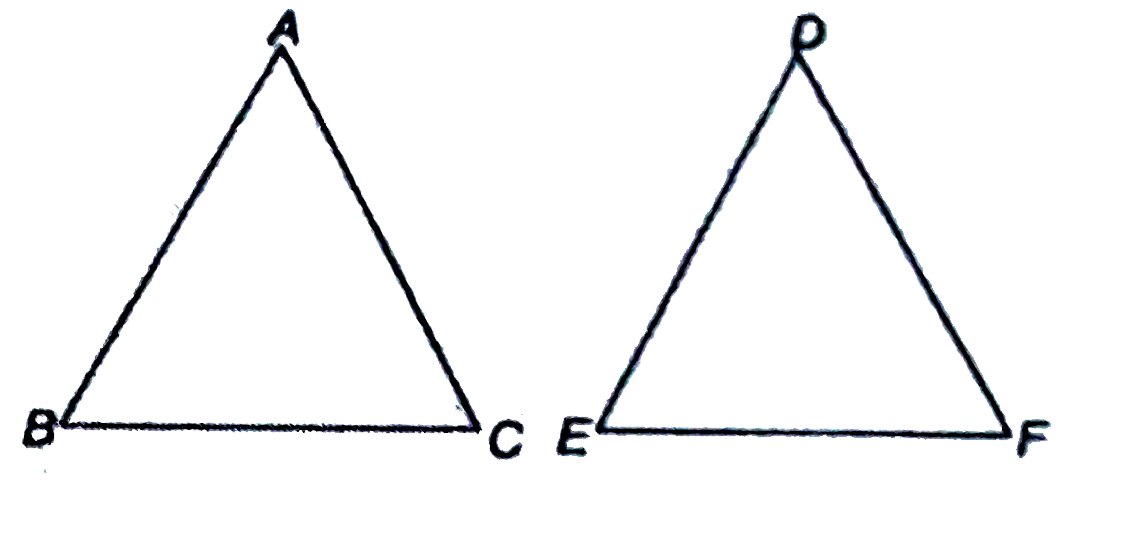
View SolutionIn figures △ABCand△DEF ar similar , the areas of △ABC is 9 sq. m and that of △DEF is 16 sq. cm. if EF= 4.2 cm, find BC.
View SolutionThe area of a circle is 1386 sq. cm, find its circumference.
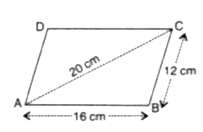
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View Solution
