If the tangents at and on = 4ax makes complimentary angles with axis then =
0
1
The correct Answer is:B
To solve the problem, we need to find the product t1t2 given that the tangents at points t1 and t2 on the parabola y2=4ax make complementary angles with the x-axis.
1. Identify the Parabola Equation:
The given equation of the parabola is:
y2=4ax
2. Find the Points on the Parabola:
The points corresponding to parameters t1 and t2 on the parabola are:
P1=(at21,2at1)andP2=(at22,2at2)
3. Write the Equation of the Tangents:
The equation of the tangent at point P1 is:
y=xt1+at1
Similarly, the equation of the tangent at point P2 is:
y=xt2+at2
4. Determine the Slopes of the Tangents:
The slopes of the tangents at points P1 and P2 are:
m1=1t1andm2=1t2
5. Use the Condition of Complementary Angles:
Since the tangents make complementary angles with the x-axis, we have:
α+β=90∘
This implies:
tan(α+β)=tan(90∘)which is undefined
6. Apply the Tangent Addition Formula:
Using the tangent addition formula:
tan(α+β)=tanα+tanβ1−tanαtanβ
Setting this equal to infinity means the denominator must be zero:
1−tanαtanβ=0
Thus:
tanαtanβ=1
7. Substituting the Slopes:
Substituting the values of the slopes:
m1⋅m2=1t1⋅1t2=1
This simplifies to:
1t1t2=1
8. Solve for t1t2:
Therefore, we have:
t1t2=1
Final Answer:
t1t2=1
The given equation of the parabola is:
y2=4ax
The points corresponding to parameters t1 and t2 on the parabola are:
P1=(at21,2at1)andP2=(at22,2at2)
The equation of the tangent at point P1 is:
y=xt1+at1
Similarly, the equation of the tangent at point P2 is:
y=xt2+at2
The slopes of the tangents at points P1 and P2 are:
m1=1t1andm2=1t2
Since the tangents make complementary angles with the x-axis, we have:
α+β=90∘
This implies:
tan(α+β)=tan(90∘)which is undefined
Using the tangent addition formula:
tan(α+β)=tanα+tanβ1−tanαtanβ
Setting this equal to infinity means the denominator must be zero:
1−tanαtanβ=0
Thus:
tanαtanβ=1
Substituting the values of the slopes:
m1⋅m2=1t1⋅1t2=1
This simplifies to:
1t1t2=1
Therefore, we have:
t1t2=1
t1t2=1
Similar Questions
Knowledge Check
If the tangent to the curve x=t2−1,y=t2−t is parallel to x-axis , then
At = 0Bt = 2Ct=12Dt=−12
If the tangents at and t1 and t2= on y2=4ax meets on its axis then
View SolutionHere T1andT2 are
View SolutionIf the chord joining the points t1and t2 on the parabola y2=4ax subtends a right angle at its vertex then t1t2=
View SolutionIf the normal at t1 on the parabola y2=4ax meet it again at t2 on the curve then t1(t1+t2)+2 = ?
View SolutionIf the chord joining t1 and t2 on the parabola y2 = 4ax is a focal chord then
View Solution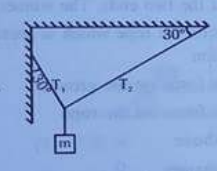
Calculate T1&T2.
View SolutionThe area of triangle formed by tangents at the parametrie points t1,t2 and t3, on y2=4ax is k|(t1−t2)(t2−t1)(t3−t1)| then K =
View Solution
