An arch is in the shape of a parabola whose axis is vertically downwords and measures 80 mts across its boltom on the ground. Its highest point is 24 mts. The measure of the horizontal beam across its cross section at a height or 18 mts is
50
40
45
60
The correct Answer is:B
To solve the problem step by step, we will derive the equation of the parabola and then find the width of the horizontal beam at a height of 18 meters.
Step 1: Understanding the Parabola
The parabola opens downwards, and we can represent it in the standard form as:
x2=−4ay
where a is a constant that determines the distance from the vertex to the focus.
Step 2: Identifying the Vertex and Points
The highest point (vertex) of the parabola is at the coordinates (0, -24) since it opens downwards and the height is given as 24 meters above the ground. The parabola is 80 meters wide at the ground level, meaning it spans from -40 to 40 on the x-axis.
Step 3: Finding the Value of a
Since the parabola passes through the point (40, 0) (the ground level), we can substitute this point into the parabola's equation to find a:
402=−4a(0+24)
This simplifies to:
1600=−4a(−24)
1600=96a
a=160096=503
Step 4: Writing the Equation of the Parabola
Now that we have a, we can write the equation of the parabola:
x2=−4(503)y
This simplifies to:
x2=−2003y
Step 5: Finding the Width at Height 18 Meters
To find the width of the beam at a height of 18 meters, we first need to find the corresponding y-coordinate:
y=−24+18=−6
Now, substitute y=−6 into the parabola's equation:
x2=−2003(−6)
This simplifies to:
x2=12003=400
Taking the square root gives:
x=±20
Step 6: Calculating the Width of the Beam
The total width of the beam at this height is:
Width=20−(−20)=20+20=40 meters
Final Answer
The measure of the horizontal beam across its cross-section at a height of 18 meters is 40 meters.
---
The parabola opens downwards, and we can represent it in the standard form as:
x2=−4ay
where a is a constant that determines the distance from the vertex to the focus.
The highest point (vertex) of the parabola is at the coordinates (0, -24) since it opens downwards and the height is given as 24 meters above the ground. The parabola is 80 meters wide at the ground level, meaning it spans from -40 to 40 on the x-axis.
Since the parabola passes through the point (40, 0) (the ground level), we can substitute this point into the parabola's equation to find a:
402=−4a(0+24)
This simplifies to:
1600=−4a(−24)
1600=96a
a=160096=503
Now that we have a, we can write the equation of the parabola:
x2=−4(503)y
This simplifies to:
x2=−2003y
To find the width of the beam at a height of 18 meters, we first need to find the corresponding y-coordinate:
y=−24+18=−6
Now, substitute y=−6 into the parabola's equation:
x2=−2003(−6)
This simplifies to:
x2=12003=400
Taking the square root gives:
x=±20
The total width of the beam at this height is:
Width=20−(−20)=20+20=40 meters
The measure of the horizontal beam across its cross-section at a height of 18 meters is 40 meters.
Similar Questions
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
View SolutionA wedge as shown in figure has a rough curved surface of coefficient of kinetic friction 1√3 whose shape can be given by equation y=x2, where the horizontal direction is x-axis, vertical direction as y axis and the end of surface O as origin and x & y are measured in meter. A small block is released, from a certain point on the surface. The maximum height of the point from where block should be released so that it does not slip.
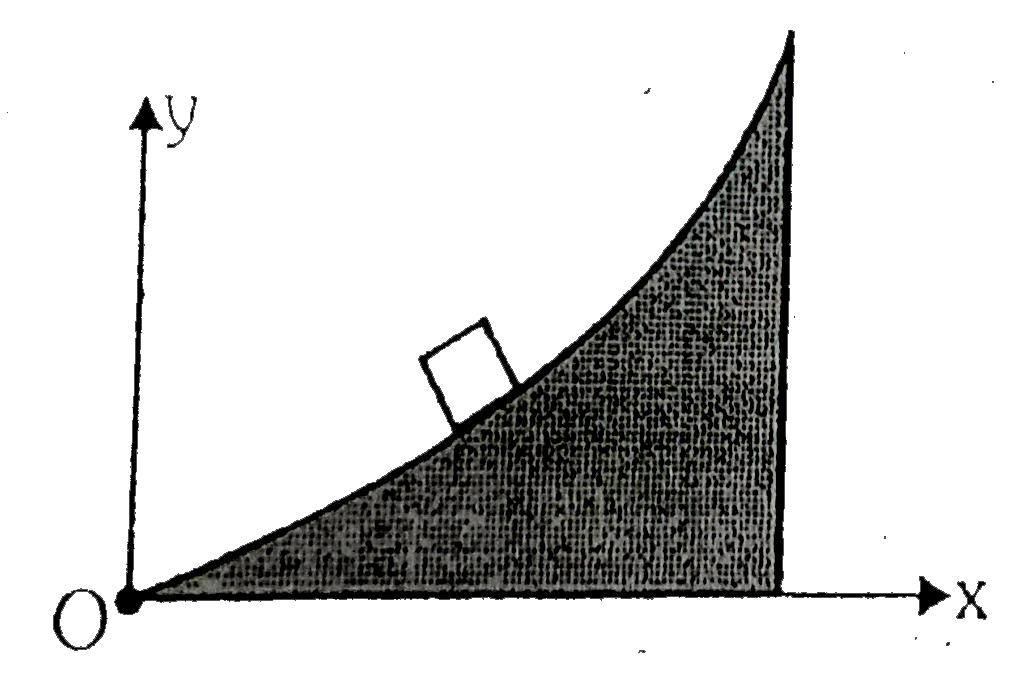
View Solution
Knowledge Check
An arch is built so that it has the shape of a parabola with the equation y=−3x2+24x where y represents the height of the arch in meters. How many times greater is the maximum height of the arch than the width of the arch at its base?
A4B6C8D10From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)
A long wire in the shape of a cylindrical shell of inner and outer radii R2 and R respectively carries a steady current I in a direction parallel to its length. This current is uniformly distributed across the area of cross-section of the wire. The magnetic field intensity at a point at a distance 3R4 from the axis of the wire is m(μ0IπR).. The value of m is _________.
View SolutionA particle is ejected from the tube at A with a velocity V at an angle θ with the verticle y-axis at a height h above the ground as shown. A strong horizontal wind gives the particle a constant horizontal acceleration a in the positive x-direction. If the particle strikes the ground at a point directly under its released position and the downward y-acceleration is taken as g then find h.

View SolutionA unifrom rod AB of length 4m and mass 12kg is thrown such that just after the projection the centre of mass of the rod moves vertically upwards with a velocity 10m/s and at the same time its is rotating with an angular velocity π2rad/sec about a horizontal axis passing through its mid point. Just after the rod is thrown it is horizontal and is as shown in the figure. Find the acceleration (in m/sec2) of the point A in m/s2 when the centre of mass is at the highest point. (Take =10m/s2 and π2=10)

View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionPulfrich refractometer is used to measure the refractive index of solids and liquid. It consist of right angled prism. A having its two faces perfectly plane. One of the face is horizontal and the other is vertical as shown is figure. The solid B whose refractive index is to be determined is taken having two faces cut perpendicular to one another. Light is incident in a direction parallel to the horizontal surface so that the light entering the prism A is at critical angle C. Finally, it emerges from the prism at an angle i. Let the refractive index of the solid be μ and that of the prism A be μ0 (which is known). Here μ0>μ and by measuring i, μ can be determinged.
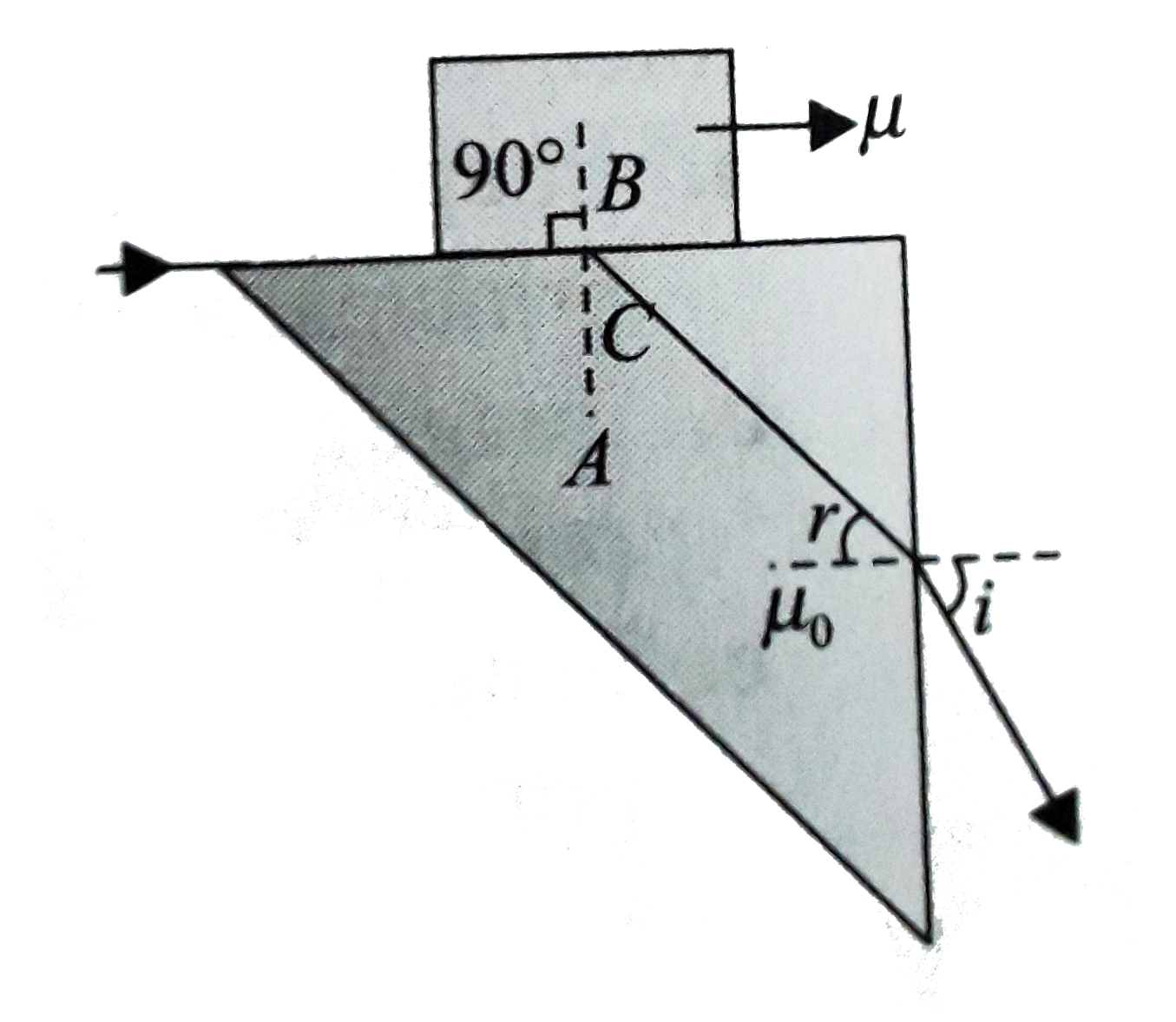
Q. Refractive index of the solid (μ) in terms of μ0 and i is
View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.
View Solution
