(1+x)25=25∑r=0Crxr then C1−C3+C5−C7+……−C25=
210
−210
212
−212
The correct Answer is:C
To solve the problem C1−C3+C5−C7+…−C25 where Cr represents the binomial coefficient (25r), we can use the properties of complex numbers and the binomial theorem.
1. Understanding the Binomial Expansion:
The binomial expansion of (1+x)25 is given by:
(1+x)25=25∑r=0Crxr
where Cr=(25r).
2. Substituting Complex Numbers:
To find the alternating sum C1−C3+C5−C7+…−C25, we can utilize the imaginary unit i (where i2=−1). We will evaluate (1+i)25 and (1−i)25.
3. Calculating (1+i)25:
Using the binomial theorem:
(1+i)25=25∑r=0Crir
This can be separated into real and imaginary parts.
4. Calculating (1−i)25:
Similarly,
(1−i)25=25∑r=0Cr(−i)r
This also separates into real and imaginary parts.
5. Adding the Two Expansions:
When we add (1+i)25 and (1−i)25:
(1+i)25+(1−i)25=212∑k=0C2k(−1)k
This gives us the sum of the even indexed coefficients.
6. Subtracting the Two Expansions:
When we subtract (1−i)25 from (1+i)25:
(1+i)25−(1−i)25=2i12∑k=0C2k+1(−1)k
This gives us the alternating sum of the odd indexed coefficients, which is precisely what we need.
7. Finding the Values:
We can express (1+i)25 and (1−i)25 using polar coordinates:
1+i=√2eiπ4⇒(1+i)25=(√2)25ei25π4=212.5ei25π4
1−i=√2e−iπ4⇒(1−i)25=(√2)25e−i25π4=212.5e−i25π4
8. Calculating the Imaginary Part:
The imaginary part of (1+i)25−(1−i)25 gives:
2i⋅212sin(25π4)
Since 25π4=6π+π4, we have:
sin(25π4)=sin(π4)=1√2
9. Final Calculation:
Thus, the final result is:
C1−C3+C5−C7+…−C25=212⋅1√2=212−0.5=211.5=212
Final Answer:
C1−C3+C5−C7+…−C25=212
The binomial expansion of (1+x)25 is given by:
(1+x)25=25∑r=0Crxr
where Cr=(25r).
To find the alternating sum C1−C3+C5−C7+…−C25, we can utilize the imaginary unit i (where i2=−1). We will evaluate (1+i)25 and (1−i)25.
Using the binomial theorem:
(1+i)25=25∑r=0Crir
This can be separated into real and imaginary parts.
Similarly,
(1−i)25=25∑r=0Cr(−i)r
This also separates into real and imaginary parts.
When we add (1+i)25 and (1−i)25:
(1+i)25+(1−i)25=212∑k=0C2k(−1)k
This gives us the sum of the even indexed coefficients.
When we subtract (1−i)25 from (1+i)25:
(1+i)25−(1−i)25=2i12∑k=0C2k+1(−1)k
This gives us the alternating sum of the odd indexed coefficients, which is precisely what we need.
We can express (1+i)25 and (1−i)25 using polar coordinates:
1+i=√2eiπ4⇒(1+i)25=(√2)25ei25π4=212.5ei25π4
1−i=√2e−iπ4⇒(1−i)25=(√2)25e−i25π4=212.5e−i25π4
The imaginary part of (1+i)25−(1−i)25 gives:
2i⋅212sin(25π4)
Since 25π4=6π+π4, we have:
sin(25π4)=sin(π4)=1√2
Thus, the final result is:
C1−C3+C5−C7+…−C25=212⋅1√2=212−0.5=211.5=212
C1−C3+C5−C7+…−C25=212
Similar Questions
(1+x)n=n∑r=0Crxr then match the following
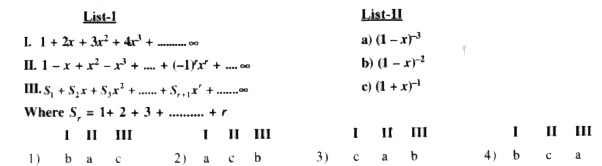
View Solutionn−1∑r=0CrCr+Cr+1=
View SolutionIf ∞∑r=1Crr!=1 then C =
View SolutionIf (1+2x+x2)n=2n∑r=0arxr ,then ar is a.(.nC2)2 b. .nCr.nCr+1 c. .2nCr d. .2nCr+1
View SolutionLet (1+x)n=n∑r=0Crxr and ,
C1C0+2C2C1+C3C2+…+nCnCn−1=1kn(n+1),
then the value of k, is
View SolutionProve that 5∑r=15Cr=31
View SolutionIf (1+x)n=n∑r=0Crxr,(1+C0C1)(1+C2C1)...(1+CnCn−1) is equal to
View SolutionIf (1+x)n=n∑r=0Crxr, then prove that C1+2C2+3C3+....+nCn=n2n−1. .
View SolutionFind the sum of n∑r=1rnCr^nCr−1 .
View SolutionIf (1+2x+x2)n=2n∑r=0arxr ,then ar is a.(.nC2)2 b. .nCr.nCr+1 c. .2nCr d. .2nCr+1
View Solution
