A circle of radius 4, is concentric with the ellipse 3x2+13y2=78. Prove that a common tangent is inclined to the major axis at an angle π4
To solve the problem, we need to show that the common tangent to the given circle and ellipse is inclined to the major axis at an angle of π4.
1. Identify the Circle's Equation:
The circle has a radius of 4 and is concentric with the ellipse. Therefore, its equation is:
x2+y2=42=16
2. Identify the Ellipse's Equation:
The equation of the ellipse is given as:
3x2+13y2=78
To convert this into standard form, we divide the entire equation by 78:
3x278+13y278=1
This simplifies to:
x226+y26=1
Here, a2=26 and b2=6.
3. Determine the Tangent Line Equations:
The equation of the tangent to the circle can be expressed as:
xcosθ+ysinθ=r
where r=4. Thus, the equation becomes:
xcosθ+ysinθ=4
The equation of the tangent to the ellipse can be expressed as:
y=mx+√a2m2+b2
Substituting a2=26 and b2=6, we get:
y=mx+√26m2+6
4. Condition for Tangency:
For the line to be a tangent to both the circle and the ellipse, the perpendicular distance from the center (0,0) to the line must equal the radius of the circle. The formula for the distance d from a point to a line Ax+By+C=0 is:
d=|Ax0+By0+C|√A2+B2
Here, for the line xcosθ+ysinθ−4=0:
- A=cosθ
- B=sinθ
- C=−4
The distance from the origin to the line is:
d=|0+0−4|√cos2θ+sin2θ=41=4
Setting this equal to the radius gives:
4=4
which is satisfied.
5. Equating the Slopes:
The slope m of the tangent line can also be derived from the ellipse's tangent condition:
√26m2+6=4√m2+1
Squaring both sides:
26m2+6=16m2+1
Cross-multiplying and simplifying:
(26m2+6)(m2+1)=16
Expanding and rearranging leads to a quadratic in m2.
6. Solving for m:
After solving the quadratic, we find:
m2=1⟹m=1 or m=−1
Thus, the slope of the tangent line is m=1.
7. Finding the Angle:
The angle θ that the tangent makes with the major axis (x-axis) is given by:
tanθ=m=1
Therefore:
θ=tan−1(1)=π4
Conclusion:
We have shown that the common tangent to the circle and the ellipse is inclined to the major axis at an angle of π4.
The circle has a radius of 4 and is concentric with the ellipse. Therefore, its equation is:
x2+y2=42=16
The equation of the ellipse is given as:
3x2+13y2=78
To convert this into standard form, we divide the entire equation by 78:
3x278+13y278=1
This simplifies to:
x226+y26=1
Here, a2=26 and b2=6.
The equation of the tangent to the circle can be expressed as:
xcosθ+ysinθ=r
where r=4. Thus, the equation becomes:
xcosθ+ysinθ=4
y=mx+√a2m2+b2
Substituting a2=26 and b2=6, we get:
y=mx+√26m2+6
For the line to be a tangent to both the circle and the ellipse, the perpendicular distance from the center (0,0) to the line must equal the radius of the circle. The formula for the distance d from a point to a line Ax+By+C=0 is:
d=|Ax0+By0+C|√A2+B2
Here, for the line xcosθ+ysinθ−4=0:
- A=cosθ
- B=sinθ
- C=−4
d=|0+0−4|√cos2θ+sin2θ=41=4
Setting this equal to the radius gives:
4=4
which is satisfied.
The slope m of the tangent line can also be derived from the ellipse's tangent condition:
√26m2+6=4√m2+1
Squaring both sides:
26m2+6=16m2+1
Cross-multiplying and simplifying:
(26m2+6)(m2+1)=16
Expanding and rearranging leads to a quadratic in m2.
After solving the quadratic, we find:
m2=1⟹m=1 or m=−1
Thus, the slope of the tangent line is m=1.
The angle θ that the tangent makes with the major axis (x-axis) is given by:
tanθ=m=1
Therefore:
θ=tan−1(1)=π4
We have shown that the common tangent to the circle and the ellipse is inclined to the major axis at an angle of π4.
Similar Questions
A circle of radius r is concentric with the ellipse x2a2+y2b2=1. Prove that the common tangent is inclined to the major axis at an angle tan−1√r2−b2a2−r2.
View SolutionA circle of radius 5√2 is concentric with the ellipse x216+y29=1, then the acute angle made by the common tangent with the line √3x−y+6=0 is
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionLength of the focal chord of the ellipse x2a2+y2b2=1 which is inclined to the major axis at angle θ is
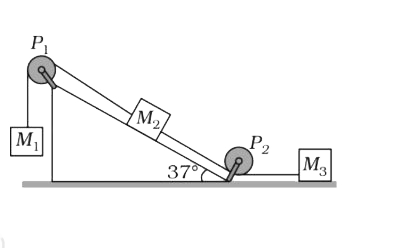
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionThe equation of tangent to the ellipse 2x2+3y2=6 which make an angle 30∘ with the major axis is
View SolutionFind the slope of a common tangent to the ellipse x2a2+y2b2=1 and a concentric circle of radius r.
View SolutionFind the equations of the tangents to the circle x2+y2=25 inclined at an angle of 60∘ to the x-axis.
View SolutionThe tangent at any point on the ellipse 16x2+25y2=400 meets the tangents at the ends of the major axis at T1 and T2. The circle on T1T2 as diameter passes through
View SolutionThe points of contact of tangents to the circle x2+y2=25 which are inclined at an angle of 30∘ to the x-axis are
View Solution
