Write the Schrodinger wave equation and explain each term in it.
Step-by-Step Solution:
1. Write the Schrödinger Wave Equation:
The Schrödinger wave equation can be expressed in two forms: the time-dependent and the time-independent forms.
- Time-Dependent Schrödinger Wave Equation:
iℏ∂Ψ∂t=^HΨ
- Time-Independent Schrödinger Wave Equation:
^HΨ=EΨ
2. Explain Each Term in the Time-Dependent Equation:
- i: This is the imaginary unit, representing the square root of -1.
- ℏ: This is the reduced Planck's constant, defined as ℏ=h2π, where h is the Planck's constant.
- Ψ: This is the wave function of the quantum system, which contains all the information about the system's state.
- ∂Ψ∂t: This term represents the partial derivative of the wave function with respect to time, indicating how the wave function changes over time.
- ^H: This is the Hamiltonian operator, which represents the total energy of the system (kinetic + potential energy).
- E: This is the energy eigenvalue associated with the wave function Ψ.
3. Explain Each Term in the Time-Independent Equation:
- ^H: Again, this is the Hamiltonian operator.
- Ψ: The wave function, which describes the quantum state of the system.
- E: The total energy of the system, which can be expressed as the sum of kinetic and potential energy.
4. Summary of the Terms:
- The Schrödinger wave equation describes the behavior of quantum systems, incorporating both wave and particle characteristics of electrons.
- The wave function Ψ provides the probability amplitude for finding a particle in a given state.
- The Hamiltonian operator ^H is crucial for determining the energy levels of the system.
The Schrödinger wave equation can be expressed in two forms: the time-dependent and the time-independent forms.
iℏ∂Ψ∂t=^HΨ
- Time-Independent Schrödinger Wave Equation:
^HΨ=EΨ
- i: This is the imaginary unit, representing the square root of -1.
- ℏ: This is the reduced Planck's constant, defined as ℏ=h2π, where h is the Planck's constant.
- Ψ: This is the wave function of the quantum system, which contains all the information about the system's state.
- ∂Ψ∂t: This term represents the partial derivative of the wave function with respect to time, indicating how the wave function changes over time.
- ^H: This is the Hamiltonian operator, which represents the total energy of the system (kinetic + potential energy).
- E: This is the energy eigenvalue associated with the wave function Ψ.
- ^H: Again, this is the Hamiltonian operator.
- Ψ: The wave function, which describes the quantum state of the system.
- E: The total energy of the system, which can be expressed as the sum of kinetic and potential energy.
- The Schrödinger wave equation describes the behavior of quantum systems, incorporating both wave and particle characteristics of electrons.
- The wave function Ψ provides the probability amplitude for finding a particle in a given state.
- The Hamiltonian operator ^H is crucial for determining the energy levels of the system.
Similar Questions
In the Schrodinger's wave equation Ψ represents
View SolutionIn the Schrodingers wave equation sπ repressents
View SolutionThe correct Schrodingers's wave equation for an electron with e as tatal energy and V as potential energy is :
View SolutionThe permissible solution to the schrodinger wave equation gives an idea of ………. Quantum number(s)
View SolutionThe correct Schrodinger's wave equation for a electron with total energy E and potential energy V is given by:
View SolutionExplain the terms:
solution
View SolutionDefine acids. Explain two chemical properties of an acid and write the chemical equation for one example of each property.
View SolutionExplain the terms rate equation and specific reaction rate.
View Solution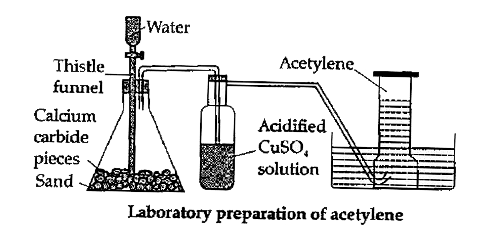
Write the equation to explain the reaction taking place in the above diagram?
View SolutionWrite equation for each conversion A to E.
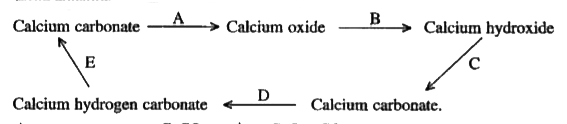
View Solution
