Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave haracter of matter has significance only for microscopic particles. De Broglie wavelength (λ) can be calculated using the relation, (λ)=hmv
where 'm' and 'v' are the mass and velocity of the particle.
Which among the following is not used to calculate the de Broglie wavelength ?
λ=cv
λ=hmv
λ=h√2Em
λ=h√2qVm
The correct Answer is:A
To solve the question regarding which among the following is not used to calculate the de Broglie wavelength, we need to analyze the de Broglie wavelength formula and the options provided.
1. Understand the de Broglie Wavelength Formula:
The de Broglie wavelength (λ) is given by the formula:
λ=hmv
where:
- h is the Planck's constant,
- m is the mass of the particle,
- v is the velocity of the particle.
2. Identify the Components:
From the formula, we can see that the calculation of the de Broglie wavelength requires:
- The mass of the particle (m)
- The velocity of the particle (v)
- Planck's constant (h)
3. Analyze the Options:
The question asks which option is not used to calculate the de Broglie wavelength. We need to evaluate the options provided (not specified in the question, but we will assume some common options based on the context).
4. Common Options:
- Option 1: λ=hmv (Used)
- Option 2: λ=h√2m⋅KE (Used, since kinetic energy is related to mass and velocity)
- Option 3: λ=h2mq (Not used, as this does not relate to the basic de Broglie wavelength formula)
- Option 4: λ=h√2m⋅qV (Used, as it relates to kinetic energy in terms of charge and voltage)
5. Conclusion:
Based on the analysis, the option that is not used to calculate the de Broglie wavelength is the one that does not relate to mass, velocity, or Planck's constant in the context of the de Broglie wavelength formula.
Final Answer:
The option that is not used to calculate the de Broglie wavelength is Option 3 (assuming it is λ=h2mq).
The de Broglie wavelength (λ) is given by the formula:
λ=hmv
where:
- h is the Planck's constant,
- m is the mass of the particle,
- v is the velocity of the particle.
From the formula, we can see that the calculation of the de Broglie wavelength requires:
- The mass of the particle (m)
- The velocity of the particle (v)
- Planck's constant (h)
The question asks which option is not used to calculate the de Broglie wavelength. We need to evaluate the options provided (not specified in the question, but we will assume some common options based on the context).
- Option 1: λ=hmv (Used)
- Option 2: λ=h√2m⋅KE (Used, since kinetic energy is related to mass and velocity)
- Option 3: λ=h2mq (Not used, as this does not relate to the basic de Broglie wavelength formula)
- Option 4: λ=h√2m⋅qV (Used, as it relates to kinetic energy in terms of charge and voltage)
Based on the analysis, the option that is not used to calculate the de Broglie wavelength is the one that does not relate to mass, velocity, or Planck's constant in the context of the de Broglie wavelength formula.
The option that is not used to calculate the de Broglie wavelength is Option 3 (assuming it is λ=h2mq).
Similar Questions
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave haracter of matter has significance only for microscopic particles. De Broglie wavelength (λ) can be calculated using the relation, (λ)=hmv
where 'm' and 'v' are the mass and velocity of the particle.
Planck's constant has same dimension as that of
View SolutionDe Broglie wavelength λ is proportional to
View SolutionThe de Broglie wavelength associated with particle is
View SolutionIf particles are moving with same velocity , then maximum de - Broglie wavelength will be for
View SolutionDe Broglie wavelength λ associated with neutrons is related with absolute temperature T as
View SolutionState how de-Broglie wavelength (λ) of moving particles varies with their linear momentum (P).
View SolutionThe de -Brogile wavelength associated with a matter particle is
View SolutionThe de -Brogile wavelength associated with a matter particle is
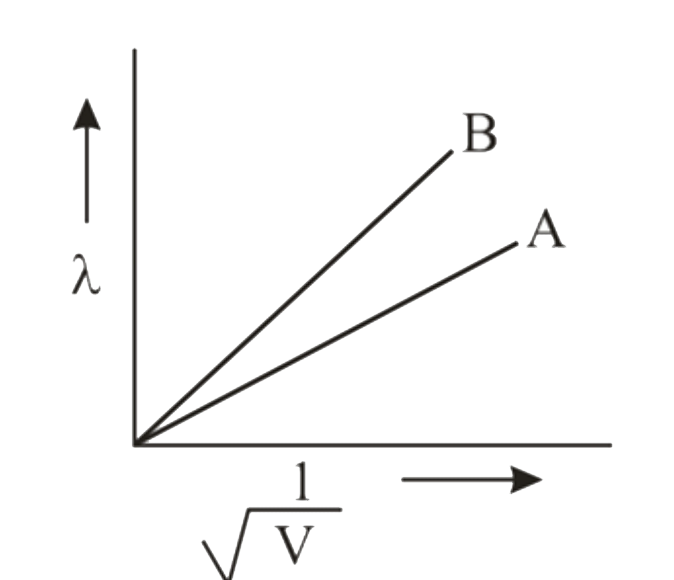
View Solutionde Broglie wavelengths of two particles A and B are plotted against (1√V) , where V is the potential on the particles. Which of the following relation is correct about the mass of the particles ?
View SolutionAn electron, an α-particle and a proton have the same kinetic energy. Which of these particles has the largest de-Broglie wavelength?
View Solution