The least count of a veriner callipers is 1100cm. The value of one division on the main scale is 1mm. The, the number of divisions on the main scale that coincide with N divisions of the vernier is
10 N
N/10
(N - 1)
N - 10
The correct Answer is:C
To solve the problem, we need to find the number of divisions on the main scale that coincide with N divisions of the vernier scale. Let's break down the solution step by step.
1. Identify the Given Information:
- Least count of the vernier calipers = 1100 cm
- Value of one division on the main scale = 1 mm = 0.1 cm
2. Understand the Relationship:
- Let M be the number of main scale divisions that coincide with N vernier scale divisions.
- The relationship can be expressed as:
M×(Value of 1 MSD)=N×(Value of 1 VSD)
- Here, (Value of 1 MSD)=0.1 cm and (Value of 1 VSD)=y (which we need to find).
3. Calculate the Least Count:
- The least count (LC) is defined as:
LC=(Value of 1 MSD)−(Value of 1 VSD)
- Given that the least count is 1100 cm, we can write:
1100=0.1−y
4. Solve for y:
- Rearranging the equation gives:
y=0.1−1100
- Convert 0.1 to a fraction:
0.1=10100
- Now substituting:
y=10100−1100=9100 cm
5. Substitute y back into the relationship:
- Now we can substitute y back into the relationship:
M×0.1=N×9100
- Rearranging gives:
M=N×9100÷0.1
- Simplifying further:
M=N×9100×101=N×910
6. Final Result:
- Therefore, the number of divisions on the main scale that coincide with N divisions of the vernier scale is:
M=N−1
Conclusion
The answer to the question is N−1.
- Least count of the vernier calipers = 1100 cm
- Value of one division on the main scale = 1 mm = 0.1 cm
- Let M be the number of main scale divisions that coincide with N vernier scale divisions.
- The relationship can be expressed as:
M×(Value of 1 MSD)=N×(Value of 1 VSD)
- Here, (Value of 1 MSD)=0.1 cm and (Value of 1 VSD)=y (which we need to find).
- The least count (LC) is defined as:
LC=(Value of 1 MSD)−(Value of 1 VSD)
- Given that the least count is 1100 cm, we can write:
1100=0.1−y
- Rearranging the equation gives:
y=0.1−1100
- Convert 0.1 to a fraction:
0.1=10100
- Now substituting:
y=10100−1100=9100 cm
- Now we can substitute y back into the relationship:
M×0.1=N×9100
- Rearranging gives:
M=N×9100÷0.1
- Simplifying further:
M=N×9100×101=N×910
- Therefore, the number of divisions on the main scale that coincide with N divisions of the vernier scale is:
M=N−1
The answer to the question is N−1.
Similar Questions
Least count of a vernier callipers is 0.01cm When the two jaws of the instrument touch each other the 5th division of the vernier scale coincide with a main scale division and the zero of the vernier scale lies to the left of the zero of the main scale. Furthermore while measuring the diameter of a sphere, the zero markof the vernier scale lies between 2.4cm and 2.5cm and the 6th vernier division coincides with a main scale division. Calculate the diameter of the sphere.
View SolutionI am a verneir Calliper. I have a task to measure the length of a pencil as shown in the figure.
The least count of my Vernier scale is 0.05 times the value of one division of main -scale.
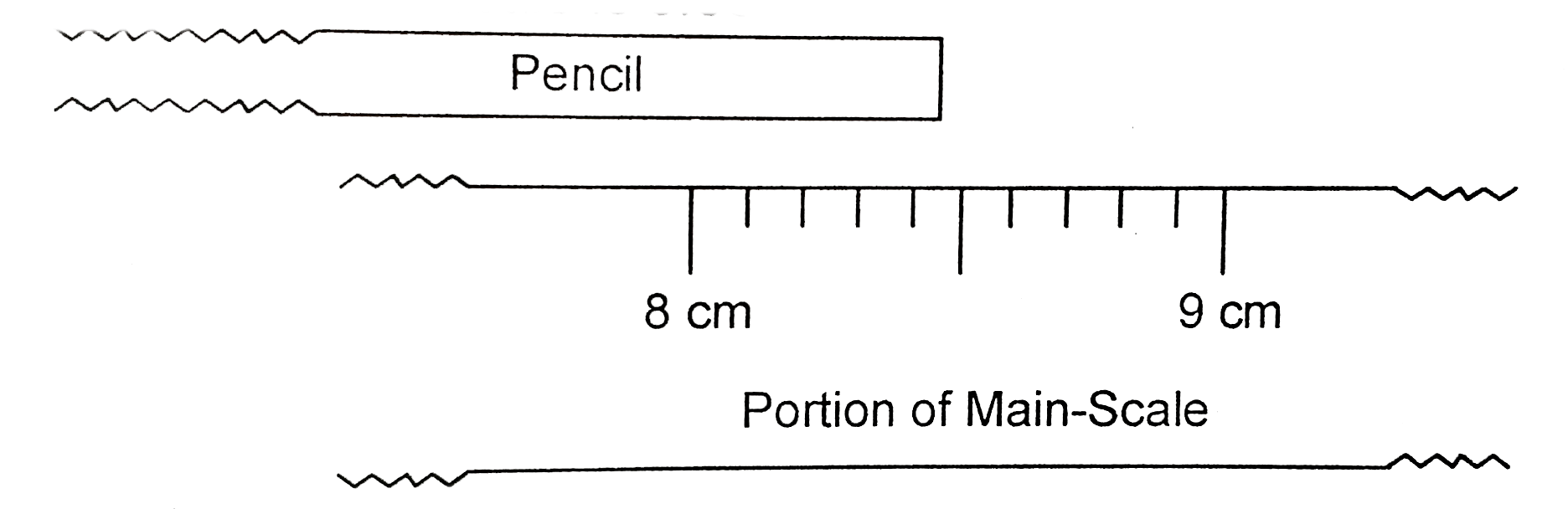
My Vernier Scale has n-divisions and coincides with (n−4) divisions of main side. While measuring the length of pencil,the n5th division of Verier-Scale exactly coincide the main scale.
Now choose the correct option (s)
View SolutionIf SandV are one main scale and one Vernier scale and n−1 divisions on the main scale are equivalent to n divisions of the Vernier , then
View SolutionThe length of an object is measured using a vernier system whose main scale is 30 cm long with 600 divisions. If 19 divisions of the main scale coincide with 20 divisions of the vernier scale, then its least count is
View SolutionIn a vernier calipers, 1cm of the main scale is divided into 20 equal parts. 19 divisions of the main scale coincide with 20 divisions on the vernier scale . Find the least count of the instrument.
View SolutionIn a vernier callipers, one main scale division is x cm and n divisions of the vernier scale coincide with (n-1) divisions of the main scale. The least count (in cm) of the callipers is :-
View SolutionThe least count of a vernier callipers is 0.01 cm and its zero error is + 0.02 cm. While measuring the length of a rod, the main scale reading is 4.8 cm and sixth division on vernier scale is in line with a marking on the main scale. Calculate the length of the rod.
View SolutionA vernier callipers having 1 main scale division =0.1cm to have a least count of 0.02cm.If n be the number of divisions on vernier scale and m be the length of vernier scale, then.
View SolutionLeast count of a vernier callipers is 0.01 cm. When the two jaws are in touch with each other, the 5th division of vernier scale coinciding with the main scale lies to the left of the zero of the main scale. Further more, while measuring the diameter of the sphere, the zero mark of the vernier lies in between 2.4 cm and 2.5 cm and ther 6th vernier division coincides with a main scale division.
View SolutionRead the special type off vernier 20 division of vernier scale are matching with 19 divisions of main scale

View Solution
