There are four vernier scales, whose observations are given in column - I and the correcponding calculations of least count are given in column - II. Match column - I with column - II appropriately. (Here S = value of IMSD : N = Value of number of divisions on vernier) (Assume ideal conditions)
Column - IColumn - II(A)S=1mm:N=10(P)0.05mm(B)S=0.5mm:N=10(Q)0.01mm(C)S=0.5mm:N=20(R)0.1mm(D)S=1mm:N=100(S)0.025mm
The correct Answer is:A-R; B-P; C-R; D-Q
To solve the problem of matching the vernier scales in Column I with their respective least counts in Column II, we will use the formula for calculating the least count of a vernier scale:
Least Count (LC) = (Value of 1 Main Scale Division (MSD)) / (Number of Vernier Scale Divisions (N))
Now, let's go through each option step by step.
Step 1: Calculate the Least Count for each Vernier Scale
(A) S = 1 mm, N = 10
- LC = 1 mm / 10 = 0.1 mm
(B) S = 0.5 mm, N = 10
- LC = 0.5 mm / 10 = 0.05 mm
(C) S = 0.5 mm, N = 20
- LC = 0.5 mm / 20 = 0.025 mm
(D) S = 1 mm, N = 100
- LC = 1 mm / 100 = 0.01 mm
Step 2: Match the Calculated Least Counts with Column II
Now that we have calculated the least counts, we can match them with the options provided in Column II:
- For (A), the least count is 0.1 mm, which corresponds to (R).
- For (B), the least count is 0.05 mm, which corresponds to (P).
- For (C), the least count is 0.025 mm, which corresponds to (S).
- For (D), the least count is 0.01 mm, which corresponds to (Q).
Final Matching
- A → R (0.1 mm)
- B → P (0.05 mm)
- C → S (0.025 mm)
- D → Q (0.01 mm)
Summary of the Matches:
- A matches with R
- B matches with P
- C matches with S
- D matches with Q
- LC = 1 mm / 10 = 0.1 mm
- LC = 0.5 mm / 10 = 0.05 mm
- LC = 0.5 mm / 20 = 0.025 mm
- LC = 1 mm / 100 = 0.01 mm
- For (B), the least count is 0.05 mm, which corresponds to (P).
- For (C), the least count is 0.025 mm, which corresponds to (S).
- For (D), the least count is 0.01 mm, which corresponds to (Q).
- B → P (0.05 mm)
- C → S (0.025 mm)
- D → Q (0.01 mm)
- A matches with R
- B matches with P
- C matches with S
- D matches with Q
Similar Questions
Match Column - I with Column - II

View SolutionMatch Column I with column II

View SolutionMatch column I with column II:

View SolutionMatch column-I with column-II

View SolutionMatch the column-I with column-II

View SolutionMatch the column I with column II
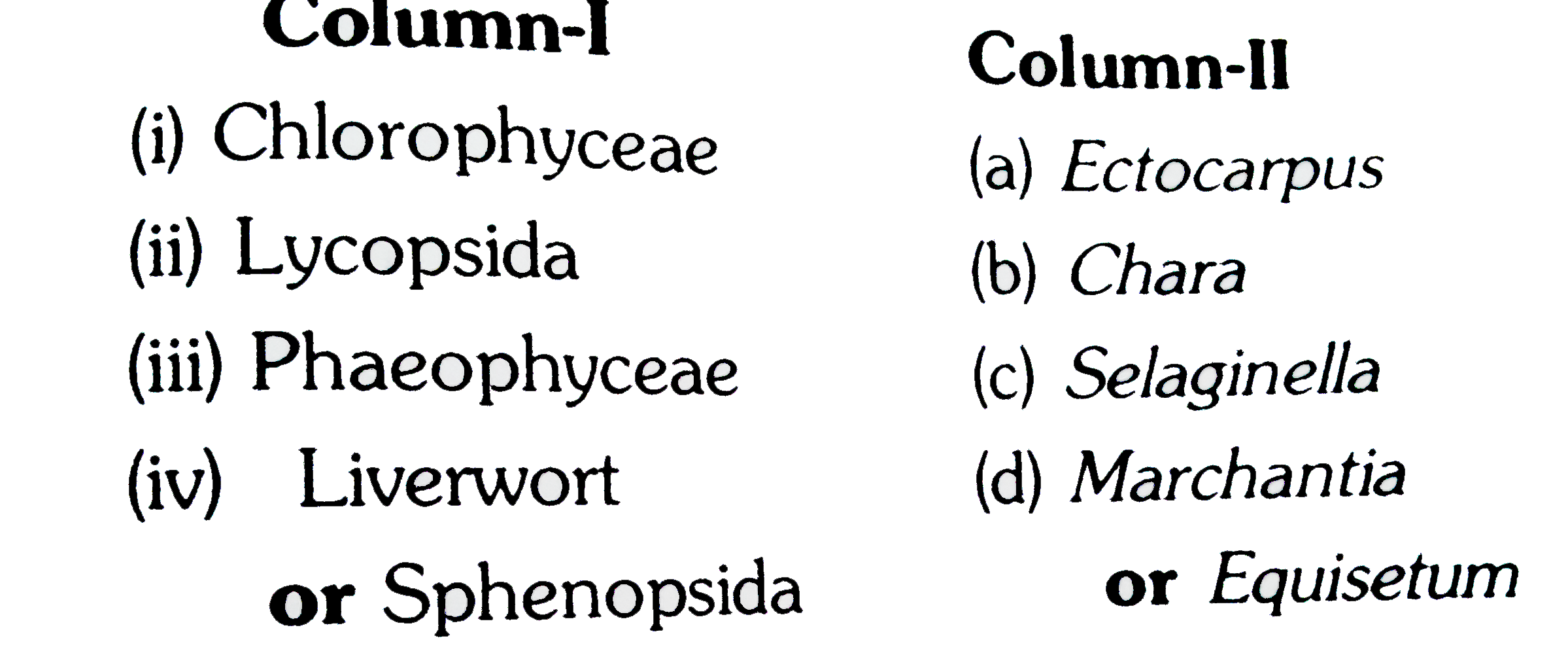
View SolutionState: Three merits of tissue culture in Plant propagation.
View SolutionMatch the column I with column II

View SolutionMatch the column-I with column-II

View SolutionMatch column-I with column-II.
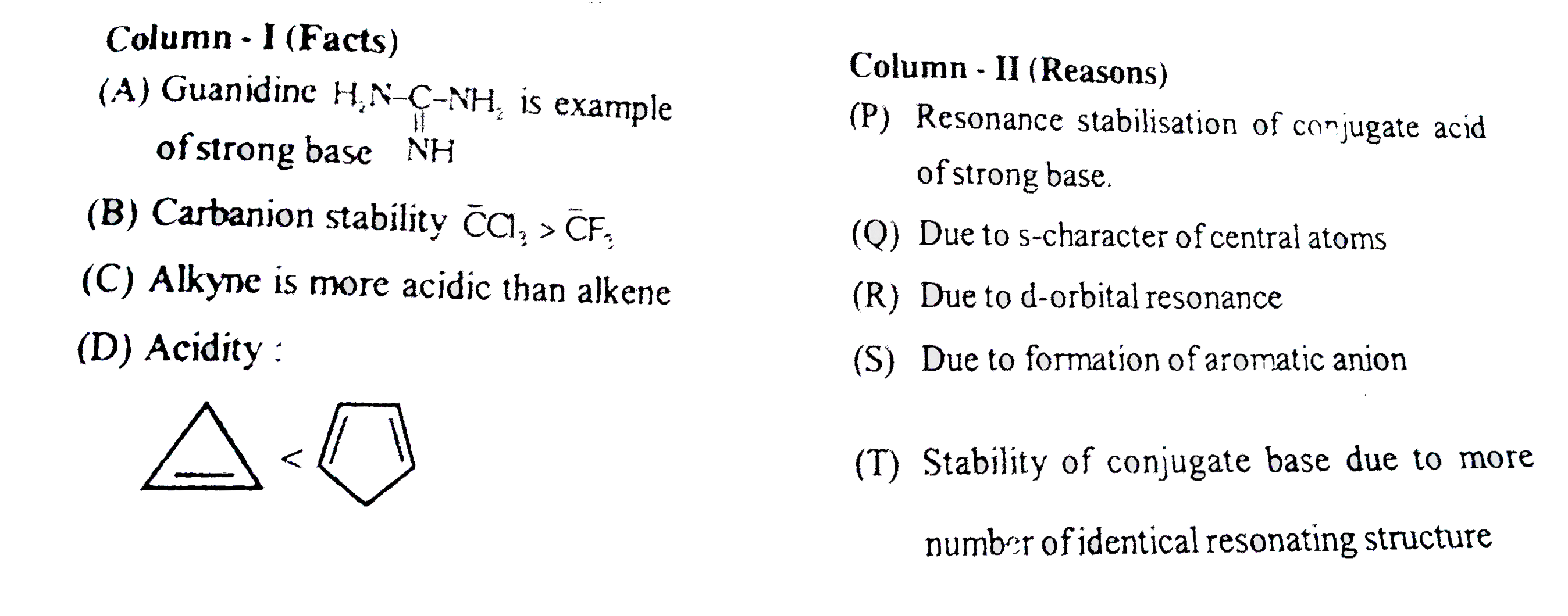 .
.
View Solution
