If n1andn2 are the frequencies of sound waves producing beats then the time interval between one maxima and next minima is
1n1+n2
1n1−n2
12(n1+n2)
12(n1−n2)
The correct Answer is:D
To solve the problem of finding the time interval between one maxima and the next minima when two sound waves with frequencies n1 and n2 produce beats, we can follow these steps:
Step 1: Understand the concept of beats
When two sound waves of slightly different frequencies interfere, they produce a phenomenon known as beats. The beat frequency is given by the absolute difference of the two frequencies:
fbeat=|n1−n2|
Step 2: Determine the time period of beats
The time period T of the beat is the reciprocal of the beat frequency:
T=1fbeat=1|n1−n2|
Step 3: Relate maxima and minima to beats
In the context of beats, one complete cycle (or one beat) consists of one maximum and one minimum. Therefore, the time interval for one complete beat (from one maximum to the next maximum) is T.
Step 4: Calculate the time interval between one maximum and the next minimum
Since one beat consists of one maximum and one minimum, the time interval between one maximum and the next minimum is half of the time period of one beat:
Time interval between one maximum and next minimum=T2=12|n1−n2|
Step 5: Final expression
Thus, the time interval between one maxima and the next minima can be expressed as:
Time interval=12(n1−n2)(assuming n1>n2)
Conclusion
The correct answer to the question is:
Time interval between one maxima and next minima=12(n1−n2)
When two sound waves of slightly different frequencies interfere, they produce a phenomenon known as beats. The beat frequency is given by the absolute difference of the two frequencies:
fbeat=|n1−n2|
The time period T of the beat is the reciprocal of the beat frequency:
T=1fbeat=1|n1−n2|
In the context of beats, one complete cycle (or one beat) consists of one maximum and one minimum. Therefore, the time interval for one complete beat (from one maximum to the next maximum) is T.
Since one beat consists of one maximum and one minimum, the time interval between one maximum and the next minimum is half of the time period of one beat:
Time interval between one maximum and next minimum=T2=12|n1−n2|
Thus, the time interval between one maxima and the next minima can be expressed as:
Time interval=12(n1−n2)(assuming n1>n2)
The correct answer to the question is:
Time interval between one maxima and next minima=12(n1−n2)
Topper's Solved these Questions
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Statement type questions:)
18 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-IA (Matching )
4 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)
10 Videos
Similar Questions
Two waves of frequencies 50 Hz and 45 Hz are produced simultaneously, then the time interval between successive maxima of the resulting wave is [maxima refers to the maximum intensity]
View SolutionWhen two waves of almost equal frequencies n1 andn2 reach at a point simultaneously, what is the time interval between successive maxima ?
View Solution
Knowledge Check
Two tuning forks of frequencies 256 and 258 vibrations/second are sounded together. Then the time interval between two consecutive maxima heard by an observer is
A2 secondB0.5 secondC250 secondD252 secondWhen two waves of almost equal frequencies v1 and v2 reach at a point simultaneously, the time interval between successive maxima is
Aυ1+υ2Bυ1−υ2C1υ1+υ2D1υ1−υ2
Two waves of frequency 500 Hz and 498 Hz are produced simultaneously. Calculate the time interval between successive maxima.
View SolutionTwo tuning forks when sounded together produce 5 beats in 2 seconds. The time interval between two successive maximum intensities of sound is
View SolutionIf n1,n2andn3 are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by
View Solution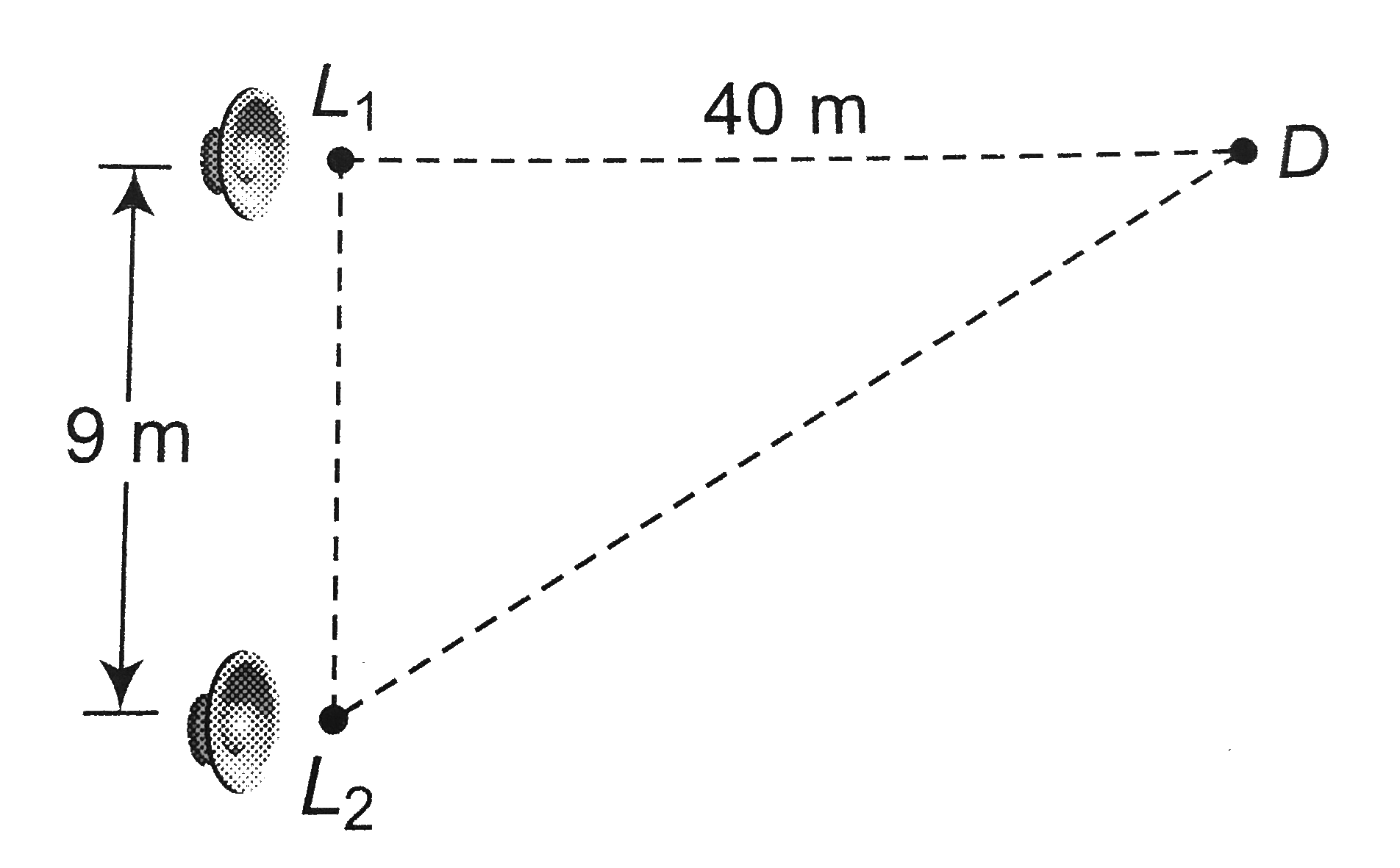
Two loudspeakers L1 and L2 driven by a common oscillator and amplifier, are arranged as shown. The frequency of the oscillator is gradually increased from zero and the detector at D records a series of maxima and minima. If the speed of sound is 330ms−1 then the frequency at which the first maximum is observed is
View Solution
Two loudspeakers L1 and L2 driven by a common oscillator and amplifier, are arranged as shown. The frequency of the oscillator is gradually increased from zero and the detector at D records a series of maxima and minima. If the speed of sound is 330ms−1 then the frequency at which the first maximum is observed is
View SolutionThe frequencies of three tuning forks A, B and C have a relation nA>nB>nC. When the forks A and B are sounded together the number of beats produced is n1 When A and C are sounded together the number of beats produced is n2 then the number of beats produced when B and C are sounded together is
View Solution
