From quantisation of angular momentum one gets for hydrogen atom, the radius of the nth orbit as rn=(n2me)(h2π)2(4πε0e2)
For a hydrogen like atom of atomic number Z,
the radius the first orbit will be the same
rn will be greater for larger 'Z' values
rnwill be smaller for larger 'Z' values
None of these
The correct Answer is:C
Step by step video & image solution for From quantisation of angular momentum one gets for hydrogen atom, the radius of the n^th orbit as r_n=((n^2)/(m_e))((h)/(2pi))^2((4piepsilon_0)/(e^2)) For a hydrogen like atom of atomic number Z, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE -IB44videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE -II35videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (ADVANCED) (Integer Type Questions)2videos
CAPACITORS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a hydrogen atom, the radius of nth bohr orbit is rn. The graph between log (rn/r1) and logn will be
A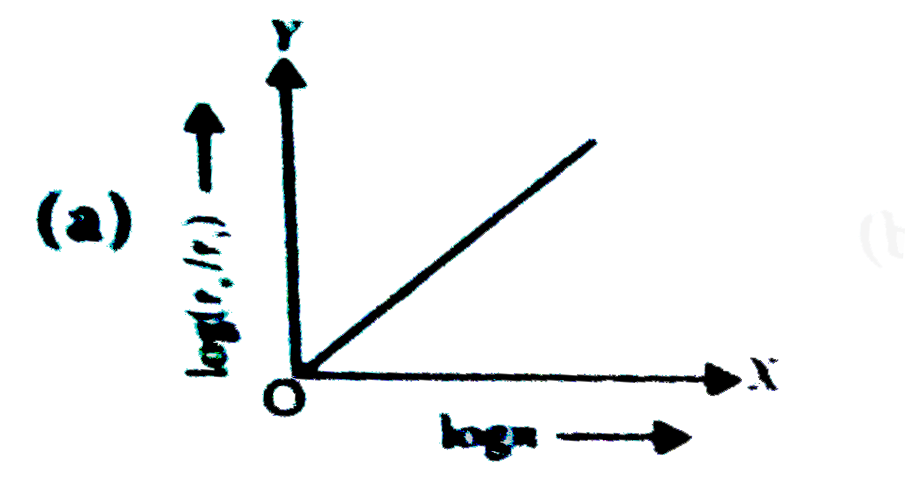 B
B C
C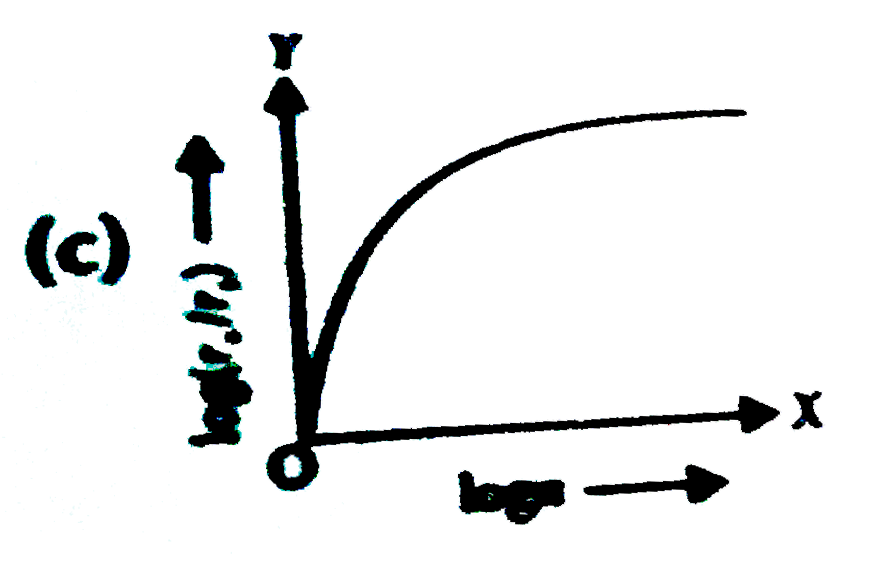 D
D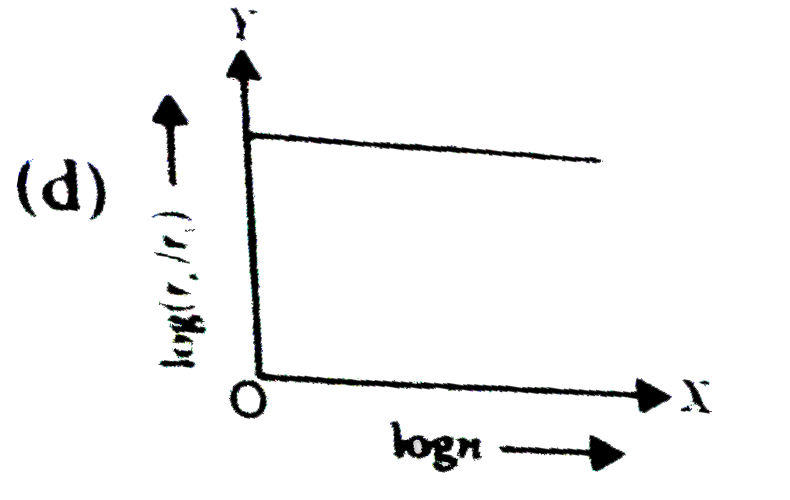
Derive Bohr's quantisation condition for angular momentum of orbiting electron in hydrogen atom using De Broglie's hypothesis.
View SolutionThe angular momentum of an electron in hydrogen atom is 4h/2π. Kinetic energy this electron is
View SolutionFind variation of angular speed and time period of single
. electron of hydrogen like atoms with n and Z.View SolutionAssertion The radius of second orbit of hydrogen atom is 2.1Å
Reason Radius of nth orbit of hydrogen atom rn∝n2View SolutionFor a Bohr atom, angular momentum of an electron is (n = 0, 1,2 .....)
View SolutionThe angular momentum of an electron in a hydrogen atom is proportional to (where n is principle quantum number )
View SolutionThe angular momentum J of the electron in a hydrogen atom is proportional to nth power of r (radius of the orbit) where n is :-
View Solution

