The graph between deBroglie wavelength (λ) and (λp) is (p is the linear momentum of the particle)

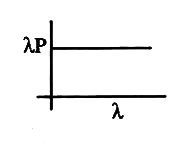


The correct Answer is:B
Step by step video & image solution for The graph between deBroglie wavelength (lamda) and (lamdap) is (p is the linear momentum of the particle) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE=II42videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
de Broglie wavelength of a moving particle is λ. Its momentum is given by :
AhλcBhλChcλDzero - Question 2 - Select One
Two particles A and B of de-broglie wavelength λ1andλ2 combine to from a particle C. The process conserves momentum. Find the de-Broglie wavelength of the particle C. (The motion is one dimensional).
AλABλAλB/(λA+λB)CλAλB/|λA−λB|Dboth (b) and ( c)
The relation between wavelength (λ) and angular wave number (k) of a wave is
View SolutionThe de-Broglie wavelength L associated with an elementary particle of linear momentum p is bets represented by the graph
View SolutionTwo particles A and B of de-broglie wavelength λ1andλ2 combine to from a particle C. The process conserves momentum. Find the de-Broglie wavelength of the particle C. (The motion is one dimensional).
View SolutionShow with the help of a labelled graph how their wavelength (λ) varies with their linear momentum (p).
View SolutionConsider the de Broglie wavelength of an electron and a proton. Which wavelength is smaller if the two particles have (a) the same speed (b) the same momentum (c) the same energy?
View SolutionElectron are accelerated through a potential difference V and protons are accelerated through a potential difference of 4 V. The de-Broglie wavelength are λeandλp for electrons and protons, respectively The ratio of λeλp is given by ( given , me is mass of electron and mp is mass of proton )
View Solution

