A projectile of mass m, charge Z., initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters. Show that for b = 0, s reduces to the closest distance of approach r0.
To solve the problem, we will use the principles of conservation of angular momentum and conservation of energy. Let's break down the solution step by step.
Step 1: Define the System
We have a projectile of mass m and charge Z′ (where Z′ is the charge of the projectile) moving with an initial speed v and an impact parameter b. It is scattered by a heavy nucleus of charge Z.
Step 2: Angular Momentum Conservation
The angular momentum L of the projectile about the nucleus is conserved. At a large distance (initially), the angular momentum is given by:
Li=mvb
At the closest distance s, the angular momentum is:
Lf=mv′s
where v′ is the speed of the projectile at the closest approach. By conservation of angular momentum:
mvb=mv′s
This simplifies to:
v′=vbs(1)
Step 3: Energy Conservation
The total mechanical energy of the system is conserved. The initial kinetic energy KEi at infinity (where the potential energy is zero) is:
KEi=12mv2
At the closest distance s, the kinetic energy KEf and potential energy PEf are given by:
KEf=12mv′2
The potential energy PEf at distance s is:
PEf=14πϵ0ZZ′e2s
By conservation of energy:
KEi+PEi=KEf+PEf
This gives us:
12mv2+0=12mv′2+14πϵ0ZZ′e2s
Step 4: Substitute v′ from Angular Momentum
Substituting v′ from equation (1) into the energy equation:
12mv2=12m(vbs)2+14πϵ0ZZ′e2s
This simplifies to:
12mv2=12mv2b2s2+14πϵ0ZZ′e2s
Step 5: Rearranging the Equation
Multiplying through by 2s2 to eliminate the fractions:
mv2s2=mv2b2+12πϵ0ZZ′e2s
Rearranging gives:
mv2s2−mv2b2−12πϵ0ZZ′e2s=0
Step 6: Quadratic Equation
This is a quadratic equation in s:
mv2s2−12πϵ0ZZ′e2s−mv2b2=0
Using the quadratic formula s=−B±√B2−4AC2A:
Here, A=mv2, B=−12πϵ0ZZ′e2, and C=−mv2b2.
Step 7: Finding the Minimum Distance s
The minimum distance s can be found using:
s=12πϵ0ZZ′e2±√(12πϵ0ZZ′e2)2+4mv2(mv2b2)2mv2
Step 8: Special Case b=0
For b=0, the equation simplifies to:
s=ZZ′e22πϵ0mv2
This is the closest distance of approach r0.
Final Formula
Thus, the formula connecting the minimum distance s of the projectile from the nucleus to the parameters is:
s=ZZ′e22πϵ0mv2
We have a projectile of mass m and charge Z′ (where Z′ is the charge of the projectile) moving with an initial speed v and an impact parameter b. It is scattered by a heavy nucleus of charge Z.
The angular momentum L of the projectile about the nucleus is conserved. At a large distance (initially), the angular momentum is given by:
Li=mvb
At the closest distance s, the angular momentum is:
Lf=mv′s
where v′ is the speed of the projectile at the closest approach. By conservation of angular momentum:
mvb=mv′s
This simplifies to:
v′=vbs(1)
The total mechanical energy of the system is conserved. The initial kinetic energy KEi at infinity (where the potential energy is zero) is:
KEi=12mv2
At the closest distance s, the kinetic energy KEf and potential energy PEf are given by:
KEf=12mv′2
The potential energy PEf at distance s is:
PEf=14πϵ0ZZ′e2s
By conservation of energy:
KEi+PEi=KEf+PEf
This gives us:
12mv2+0=12mv′2+14πϵ0ZZ′e2s
Substituting v′ from equation (1) into the energy equation:
12mv2=12m(vbs)2+14πϵ0ZZ′e2s
This simplifies to:
12mv2=12mv2b2s2+14πϵ0ZZ′e2s
Multiplying through by 2s2 to eliminate the fractions:
mv2s2=mv2b2+12πϵ0ZZ′e2s
Rearranging gives:
mv2s2−mv2b2−12πϵ0ZZ′e2s=0
This is a quadratic equation in s:
mv2s2−12πϵ0ZZ′e2s−mv2b2=0
Using the quadratic formula s=−B±√B2−4AC2A:
Here, A=mv2, B=−12πϵ0ZZ′e2, and C=−mv2b2.
The minimum distance s can be found using:
s=12πϵ0ZZ′e2±√(12πϵ0ZZ′e2)2+4mv2(mv2b2)2mv2
For b=0, the equation simplifies to:
s=ZZ′e22πϵ0mv2
This is the closest distance of approach r0.
Thus, the formula connecting the minimum distance s of the projectile from the nucleus to the parameters is:
s=ZZ′e22πϵ0mv2
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE - I20videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE - II19videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - EXERCISE -III25videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - PRACTICE SHEET (ADVANCED) (Integer Type Questions)2videos
CAPACITORS
Similar Questions
When an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
View SolutionWhen an α−particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closest approach from the nucleus depends on m as :
View SolutionWhen an α−particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closest approach from the nucleus depends on m as :
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing, decreasing or constant.
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
View Solution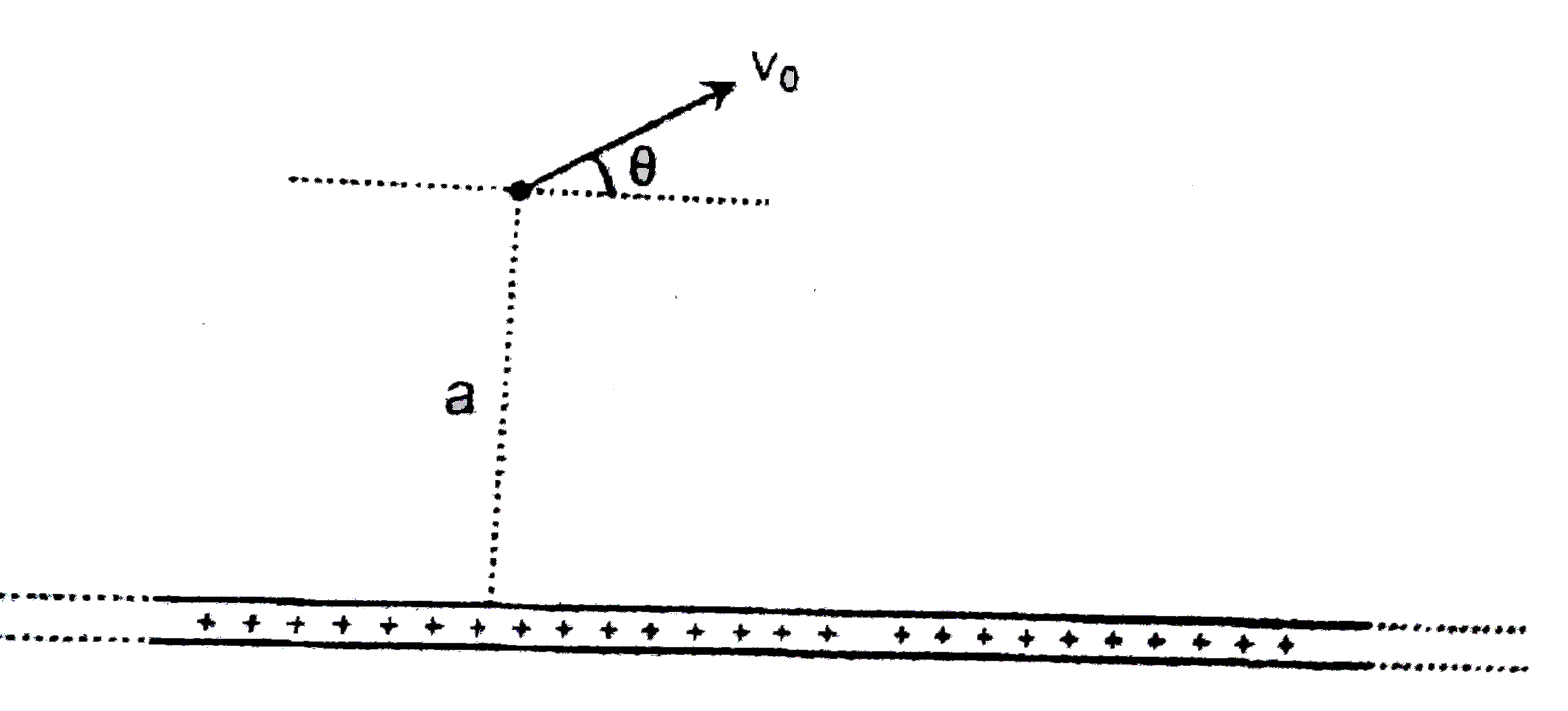
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε20/qλ). The value of n is (ingnore gravity)View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
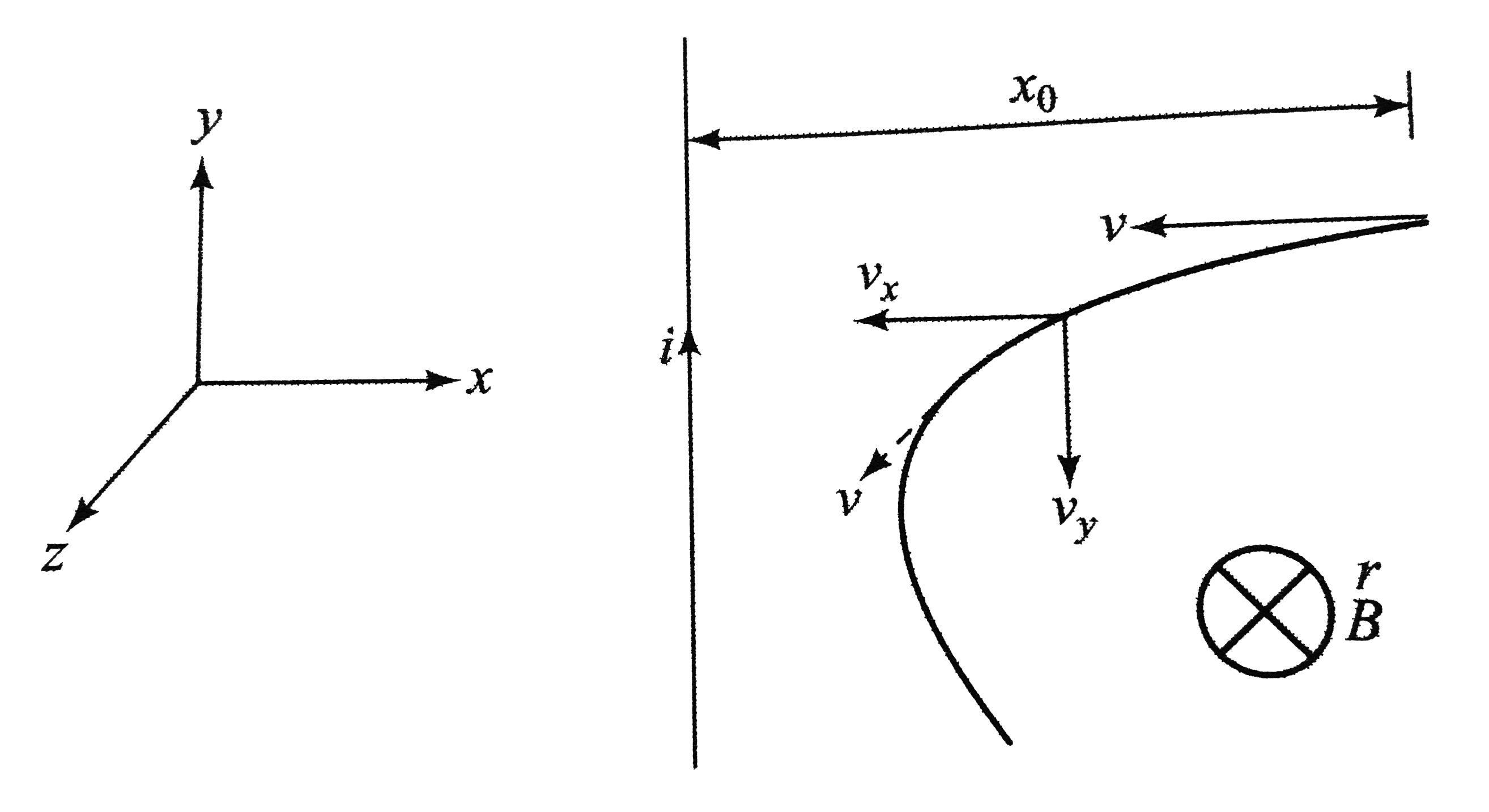
 View Solution
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as
 View Solution
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The limiting electric potential of the sphere isView SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The total energy (E) of a proton in the beam travelling with seed v at a distance of r(r≥R) from point O. Assuming that the sphere has acquired an electrostatic charge Q isView Solution

