The charges - q, Q, -q are placed along x-axis at x = 0, x = a and x = 2a. If the potential energy of the system is zero, then Q:q is
1:2
2:1
1:4
4:1
The correct Answer is:C
To solve the problem, we need to find the ratio Qq such that the potential energy of the system of charges is zero. We have three charges: −q at x=0, Q at x=a, and −q at x=2a.
1. Identify the positions and charges:
- Charge −q is at x=0
- Charge Q is at x=a
- Charge −q is at x=2a
2. Calculate the potential energy U of the system:
The potential energy U of a system of point charges is given by the formula:
U=k∑i<jqiqjrij
where k=14πϵ0.
3. Calculate the potential energy contributions:
- The potential energy between −q at x=0 and Q at x=a:
U1=−qQa
- The potential energy between Q at x=a and −q at x=2a:
U2=−qQa
- The potential energy between the two −q charges at x=0 and x=2a:
U3=(−q)(−q)2a=q22a
4. Combine the potential energy contributions:
The total potential energy U of the system is:
U=U1+U2+U3=−qQa+−qQa+q22a
Simplifying this gives:
U=−2qQa+q22a
5. Set the total potential energy to zero:
According to the problem, the potential energy U is zero:
−2qQa+q22a=0
6. Multiply through by 2a to eliminate the denominator:
−4qQ+q2=0
7. Rearranging gives:
q2=4qQ
8. Divide both sides by q (assuming q≠0):
q=4Q
9. Express Qq:
Qq=14
Final Answer:
Thus, the ratio Qq is 14.
- Charge −q is at x=0
- Charge Q is at x=a
- Charge −q is at x=2a
The potential energy U of a system of point charges is given by the formula:
U=k∑i<jqiqjrij
where k=14πϵ0.
- The potential energy between −q at x=0 and Q at x=a:
U1=−qQa
- The potential energy between Q at x=a and −q at x=2a:
U2=−qQa
- The potential energy between the two −q charges at x=0 and x=2a:
U3=(−q)(−q)2a=q22a
The total potential energy U of the system is:
U=U1+U2+U3=−qQa+−qQa+q22a
Simplifying this gives:
U=−2qQa+q22a
According to the problem, the potential energy U is zero:
−2qQa+q22a=0
−4qQ+q2=0
q2=4qQ
q=4Q
Qq=14
Thus, the ratio Qq is 14.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)
28 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTION)
1 Video
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (MAIN) INTEGER TYPE QUESTIONS
2 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
Three charges are placed along x- axis at x=−a,x=0 and x=a as shown . Calculate the potential energy of the system.

View SolutionThree charges are placed along x-axis at x = - a x = 0 and x = a as shown in the figure. The potential energy of the system is

View SolutionThree charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ is
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
View SolutionSet up arrangment of three point charges : q,+2qandxq separated by equal finite distances so that electric potential energy of the system is zero. What is x ?
View SolutionA point charge q1=4.00nC is placed at the origin, and a second point charge q2=−3.00nC, placed on the x-axis at x = + 20.0 cm. A third point charge q3=2.00nC is placed on the X-axis between q1,andq2. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if q3 is placed at x= + 10.0 cm?
(b) Where should q3 be placed to make the potential energy of the system equal to zero?
View SolutionThree charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
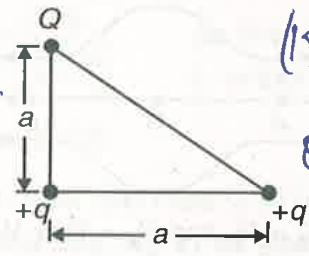
View SolutionTwo equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View Solution