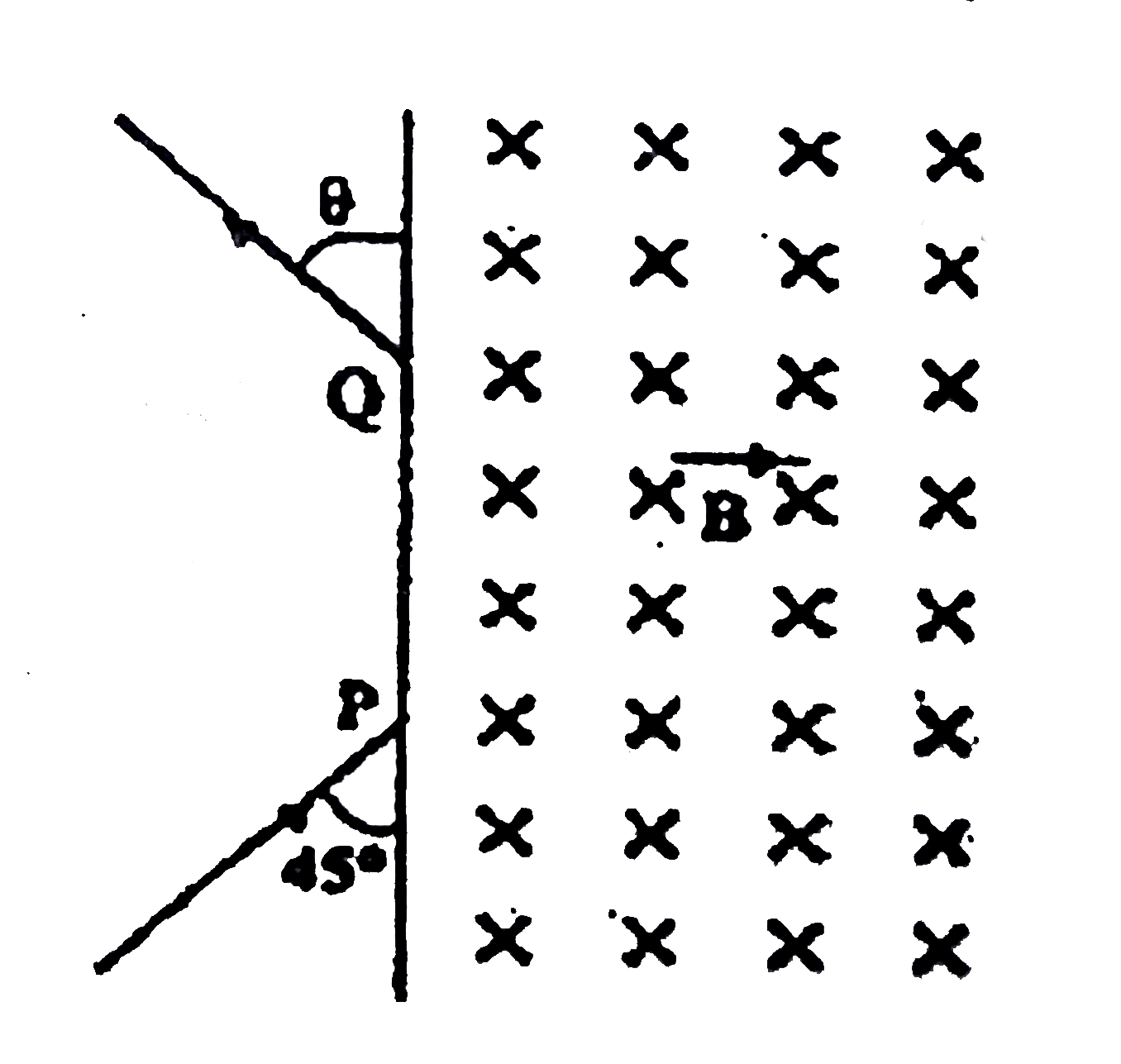
A particle of mass m=1.6×10−27 kg and charge q=1.6×10−19C enters a region of uniform magnetic field of stregth 1T along the direction shown in figure. The speed of the particle is 107m/s
a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point F. Find the distasnce EF and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at E.
Inside a magnetic field speed of charged particle does not change. Further, velocity is perpendicular to magnetic field in both the cases hence path of the particle in the magnetic field will be circular. Centre of circle can be obtained by drawing perpendiculars to velocity ( or tangent to the circular path) at E and F. Radius and angular speed of circular path would be
r=mvBq and ω=Bqm
A) Refer figure (a) : ∠CFG=90∘−θ and ∠=90∘−45∘=45∘, Since CF=CE
∴∠CFG=∠CEG or 90∘−θ=45∘ or θ=45∘
Further, FG=GE=Rcos45°∴EF=2FG=2rcos45°
=2mvcoss45∘Bq=2(1.6×10−27)(1√2)(1)(1.6×10−19)=0.14m
In this case particle completes 14th of circle in the magnetic field
B) Refer figure (b) : In this case particle will complete 34 th of circle in the magnetic field. Hence, the time spent in the magnetic field.
t=34 (time period of circular motion)
=34(2πmBq)=3πm2Bq=(3π)(1.6×1027)(2)(1)(1.6×10−19)=4.712×10−8s
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
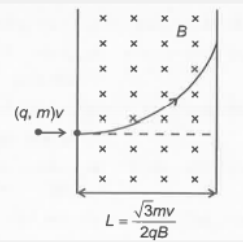View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
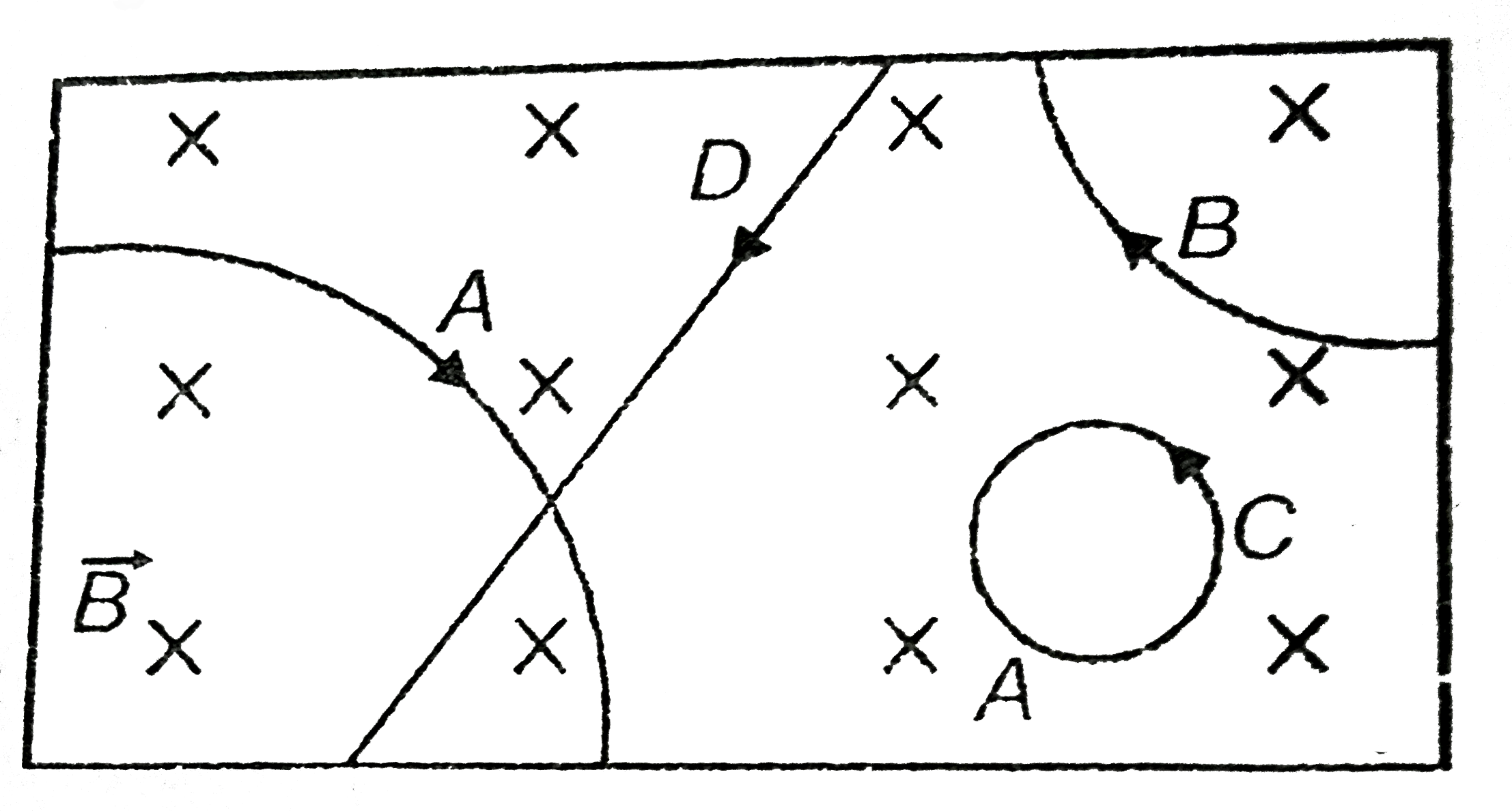View SolutionA particule having charge q enters a rection of untiormal magnetic field B (direction inwards) and in denfectro as shown . The magnetic of the momentum of the particles is
View SolutionA particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular pathView SolutionA small particle of mass m = 1 kg and charge of 1C enters perpendicularly in a triangular region of uniform magnetic field of strength 2T as shown in figure :
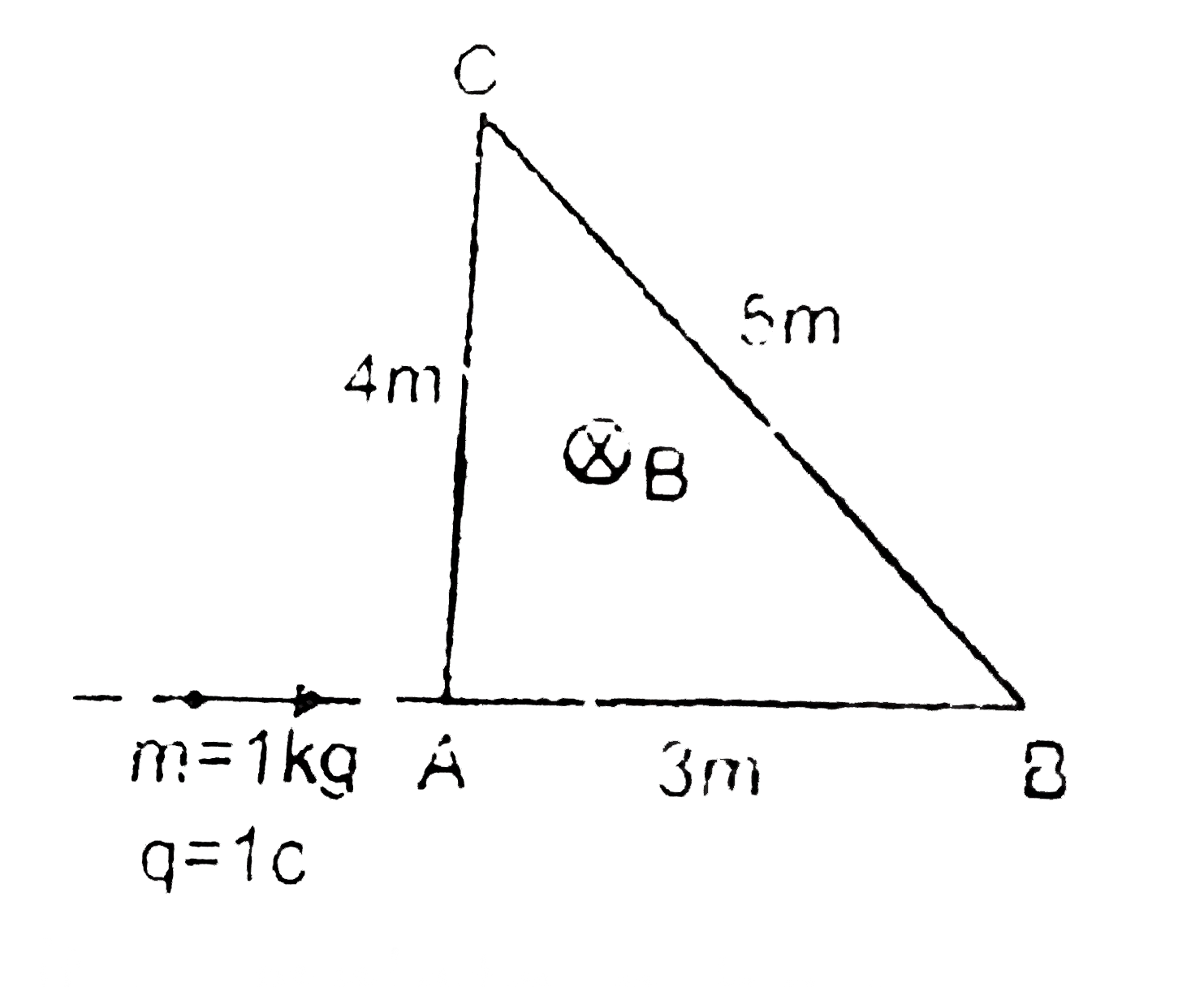
Calculate maximum velocity of the particle with which it should enter so that it complete a half-circle in magnetic region :View SolutionA small particle of mass m = 1 kg and charge of 1C enters perpendicularly in a triangular region of uniform magnetic field of strength 2T as shown in figure :
Calculate maximum velocity of the particle with which it should enter so that it complete a half-circle in magnetic region :View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View Solution