A rough inclined plane inclined at angle 37° with horizontal, has a metallic wire of length 20cm with its length ⊥ to length, of inclined plane (μ=0.1) When a current of i is passing through the wire and a magnetic field is applied normal to the plane upwards, the wire starts moving up with uniform velocity for B = 0.5T. Then find the magnitude of current i, (mass of the wire=50g)
To solve the problem, we need to analyze the forces acting on the metallic wire on the inclined plane and apply the principles of physics to find the magnitude of the current i.
1. Identify the Forces Acting on the Wire:
- The weight of the wire W=mg acts downwards, where m=50g=0.05kg and g=10m/s2.
- The weight can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
- The frictional force Ff acts down the incline and is given by Ff=μN, where N is the normal force.
2. Calculate the Normal Force:
- The normal force N is equal to the perpendicular component of the weight:
N=mgcosθ
3. Calculate the Frictional Force:
- Using μ=0.1:
Ff=μN=μ(mgcosθ)=0.1(mgcos37∘)
4. Magnetic Force Acting on the Wire:
- The magnetic force FB acting on the wire due to the magnetic field B is given by:
FB=BILsinθ
- Since the wire is perpendicular to the magnetic field, sinθ=1:
FB=BIL
5. Set Up the Equation of Motion:
- Since the wire moves with uniform velocity, the net force acting on it is zero:
FB=mgsinθ+Ff
- Substituting the expressions for FB and Ff:
BIL=mgsinθ+μ(mgcosθ)
6. Substitute Known Values:
- Given:
- B=0.5T
- L=20cm=0.2m
- m=0.05kg
- g=10m/s2
- θ=37∘ (where sin37∘=35 and cos37∘=45)
- Plugging in these values:
0.5⋅i⋅0.2=(0.05⋅10)⋅35+0.1⋅(0.05⋅10)⋅45
7. Calculate Each Term:
- The left side:
0.5⋅i⋅0.2=0.1i
- The right side:
(0.5)⋅35+0.1⋅(0.5)⋅45=0.3+0.08=0.38
8. Equate and Solve for i:
0.1i=0.38
i=0.380.1=3.8A
Final Answer:
The magnitude of the current i is 3.8A.
- The weight of the wire W=mg acts downwards, where m=50g=0.05kg and g=10m/s2.
- The weight can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
- The frictional force Ff acts down the incline and is given by Ff=μN, where N is the normal force.
- The normal force N is equal to the perpendicular component of the weight:
N=mgcosθ
- Using μ=0.1:
Ff=μN=μ(mgcosθ)=0.1(mgcos37∘)
- The magnetic force FB acting on the wire due to the magnetic field B is given by:
FB=BILsinθ
- Since the wire is perpendicular to the magnetic field, sinθ=1:
FB=BIL
- Since the wire moves with uniform velocity, the net force acting on it is zero:
FB=mgsinθ+Ff
- Substituting the expressions for FB and Ff:
BIL=mgsinθ+μ(mgcosθ)
- Given:
- B=0.5T
- L=20cm=0.2m
- m=0.05kg
- g=10m/s2
- θ=37∘ (where sin37∘=35 and cos37∘=45)
0.5⋅i⋅0.2=(0.05⋅10)⋅35+0.1⋅(0.05⋅10)⋅45
- The left side:
0.5⋅i⋅0.2=0.1i
- The right side:
(0.5)⋅35+0.1⋅(0.5)⋅45=0.3+0.08=0.38
0.1i=0.38
i=0.380.1=3.8A
The magnitude of the current i is 3.8A.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A long wire carrying a current i=2A is bent at right angles . The magnetic field lying on a perpendicular normal to the plane of the wire draw through the point of bending at distance 1 m form it is ………….Tesla.
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
 View Solution
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA loop of flexible conducting wire of length l lies in magnetic field B which is normal to the plane of loop. A current l is passed through the loop. The tension developed in the wire to open up is
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
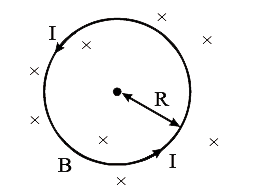 View Solution
View SolutionA current of 1 A flows a wire of length 0.1 m in a magnetic field of 0.5 T. The force acting on the wire when it makes an angle of 90∘ with the field is
View SolutionA wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire
 View Solution
View SolutionThe figure shows a conductor of weight 1.0N& length L=0.5m placed on a rough inclined plane making an angle 30∘ with the horizontal so that conductor is perpendicular to a uniform horizontal magnetic field of induction B=0.10T.The coefficient of static friction betwen the conductor inside the plane of is 0.1. A current of l=10A flows through the conductor inside the plane of this paper as shown.What is the force needed to be applied parallel to the inclined plane to keep the conductor at rest?
 View Solution
View SolutionA rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient offriction between chain and inclined plane is μ, the maximum length of the lianging part to prevent the chain from falling vertically is:
View Solution

