A straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
0.2 gauss
0.3 gauss
0.4 gauss
0.5 gauss
The correct Answer is:C
To solve the problem, we will use the formula for the magnetic field (magnetic induction) produced by a straight current-carrying conductor at a point perpendicular to it. The formula is given by:
B=μ0I4πr(sinθ1+sinθ2)
Where:
- B is the magnetic induction,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes,
- r is the perpendicular distance from the midpoint of the conductor to the point where the magnetic field is being calculated,
- θ1 and θ2 are the angles made by the line connecting the ends of the conductor to the point with the perpendicular line.
1. Identify the given values:
- Length of the conductor, L=32cm=0.32m
- Current, I=30A
- Perpendicular distance from the midpoint, r=12cm=0.12m
2. Calculate the half-length of the conductor:
L2=0.322=0.16m
3. Determine the angles θ1 and θ2:
Since the point is at the midpoint and the conductor is straight, θ1=θ2. We can use the right triangle formed by the conductor and the point to find sinθ1:
sinθ1=oppositehypotenuse=0.16√(0.16)2+(0.12)2
Calculate the hypotenuse:
√(0.16)2+(0.12)2=√0.0256+0.0144=√0.04=0.2m
Therefore,
sinθ1=0.160.2=0.8
4. Substitute the values into the magnetic induction formula:
Since sinθ1=sinθ2,
B=μ0I4πr(2sinθ1)=(4π×10−7)×304π×0.12(2×0.8)
Simplifying,
B=(4×10−7)×300.12×1.6
5. Calculate the value:
B=1.2×10−50.12×1.6=1.0×10−5×1.6=1.6×10−5T
Converting to Gauss (1 T = 10^4 Gauss),
B=1.6×10−5×104=0.16Gauss
6. Final answer:
The magnetic induction at the point is approximately 0.16Gauss.
- B is the magnetic induction,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes,
- r is the perpendicular distance from the midpoint of the conductor to the point where the magnetic field is being calculated,
- θ1 and θ2 are the angles made by the line connecting the ends of the conductor to the point with the perpendicular line.
- Length of the conductor, L=32cm=0.32m
- Current, I=30A
- Perpendicular distance from the midpoint, r=12cm=0.12m
L2=0.322=0.16m
Since the point is at the midpoint and the conductor is straight, θ1=θ2. We can use the right triangle formed by the conductor and the point to find sinθ1:
sinθ1=oppositehypotenuse=0.16√(0.16)2+(0.12)2
Calculate the hypotenuse:
√(0.16)2+(0.12)2=√0.0256+0.0144=√0.04=0.2m
Therefore,
sinθ1=0.160.2=0.8
Since sinθ1=sinθ2,
B=μ0I4πr(2sinθ1)=(4π×10−7)×304π×0.12(2×0.8)
Simplifying,
B=(4×10−7)×300.12×1.6
B=1.2×10−50.12×1.6=1.0×10−5×1.6=1.6×10−5T
Converting to Gauss (1 T = 10^4 Gauss),
B=1.6×10−5×104=0.16Gauss
The magnetic induction at the point is approximately 0.16Gauss.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II79videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
The magnituge of 'B' from a conductor carrying 35A at a perpendicular distance of 20cm from it, in tesla is
View SolutionFigure shows a straight wire of length a carrying a current I. What is the magnitude of magnetic field induction produced by the current at P, which is lying at a perpendicular distance a from one end of the wire.

 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conductor of length 2 m carrying current 2 A is held parallel to an infinitely long conductor carrying current of 12 A at a distance of 100 mm, the force on small conductor is
A8.6×10−5NB6.6×10−5NC7.6×10−5ND9.6×10−5N
Find the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionA conductor is carrying a current i. the magnetic field intensity at a the point O which is the common centre of three arcs is
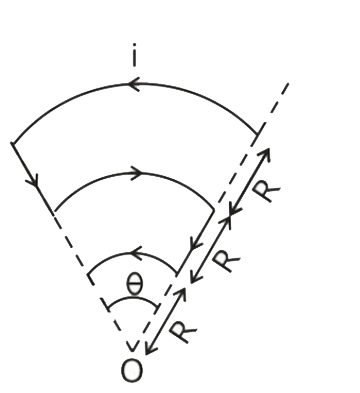 View Solution
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View SolutionA wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire
 View Solution
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View Solution

