Construct the reflected wavefront when a plane wavefront is incident on a plane reflecting surface. Hence, explain the laws of reflection. Why does an expanding spherical wave continue to expand outward from the source?
Step-by-Step Solution:
Step 1: Understand the Incident Wavefront
- Begin by considering a plane wavefront that is incident on a plane reflecting surface. A wavefront is a surface over which the wave has a constant phase. For a plane wavefront, the wavefronts are parallel lines.
Step 2: Draw the Reflecting Surface
- Draw a horizontal line to represent the plane reflecting surface. This line will act as the boundary where the wavefront will reflect.
Step 3: Indicate the Incident Wavefront
- Draw the incident wavefront approaching the reflecting surface. Label the points on the wavefront as I1, I2, etc. This wavefront is perpendicular to the direction of wave propagation.
Step 4: Draw the Normal Line
- At the point where the incident wavefront meets the reflecting surface, draw a normal line (a perpendicular line) to the surface. This normal line is crucial for measuring angles of incidence and reflection.
Step 5: Construct the Reflected Wavefront
- After the wavefront hits the reflecting surface, it will reflect. Draw the reflected wavefront, which will also be a set of parallel lines but in the opposite direction. Label this reflected wavefront as R1, R2, etc.
Step 6: Apply Huygens' Principle
- According to Huygens' Principle, every point on the wavefront acts as a source of secondary wavelets. When the incident wavefront reaches the reflecting surface, each point on the surface acts as a source of new wavelets that propagate in the reflected direction.
Step 7: State the Laws of Reflection
- The laws of reflection state:
1. The angle of incidence (i) is equal to the angle of reflection (r). This can be expressed as i = r.
2. The incident wavefront, the reflected wavefront, and the normal to the surface all lie in the same plane.
Step 8: Explain the Expansion of Spherical Waves
- An expanding spherical wave continues to expand outward from its source. This is because as the wave propagates, the surface area of the sphere increases with the square of the radius (A = 4πr²). Consequently, the intensity of the wave (which is the power per unit area) decreases as it moves away from the source, following the inverse square law (Intensity ∝ 1/r²).
- Begin by considering a plane wavefront that is incident on a plane reflecting surface. A wavefront is a surface over which the wave has a constant phase. For a plane wavefront, the wavefronts are parallel lines.
- Draw a horizontal line to represent the plane reflecting surface. This line will act as the boundary where the wavefront will reflect.
- Draw the incident wavefront approaching the reflecting surface. Label the points on the wavefront as I1, I2, etc. This wavefront is perpendicular to the direction of wave propagation.
- At the point where the incident wavefront meets the reflecting surface, draw a normal line (a perpendicular line) to the surface. This normal line is crucial for measuring angles of incidence and reflection.
- After the wavefront hits the reflecting surface, it will reflect. Draw the reflected wavefront, which will also be a set of parallel lines but in the opposite direction. Label this reflected wavefront as R1, R2, etc.
- According to Huygens' Principle, every point on the wavefront acts as a source of secondary wavelets. When the incident wavefront reaches the reflecting surface, each point on the surface acts as a source of new wavelets that propagate in the reflected direction.
- The laws of reflection state:
1. The angle of incidence (i) is equal to the angle of reflection (r). This can be expressed as i = r.
2. The incident wavefront, the reflected wavefront, and the normal to the surface all lie in the same plane.
- An expanding spherical wave continues to expand outward from its source. This is because as the wave propagates, the surface area of the sphere increases with the square of the radius (A = 4πr²). Consequently, the intensity of the wave (which is the power per unit area) decreases as it moves away from the source, following the inverse square law (Intensity ∝ 1/r²).
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )24videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )53videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
A plane wavefront incident on a reflecting surface at an angle of 30∘ with horizontal. Find the angle of reflected wavefront with horizontal
View SolutionA plane wavefront incident on a reflecting surface at and angle of 30∘ with vertical. Find the angle (acute) of reflected wave with vertical.
View Solution
Knowledge Check
- Question 1 - Select One
Unpolarized light is incident on a plane glass surface. The angle of incidence so that reflected and refracted rays and perpendicular to each other, then
Ataniβ=μ2Btaniβ=μCsiniβ=μDcosiβ=μ
A plane wavefront AB is incident on a concave mirror as shown. Then,the reflected wavefront will be
 View Solution
View SolutionPlane wavefronts are incident on a spherical mirror as shown, the reflected wavefronts will be
 View Solution
View SolutionUse Huygen's principle to show how a plane wavefront propagates from a denser to rarer medium. Hence verift snell's law of refreaction.
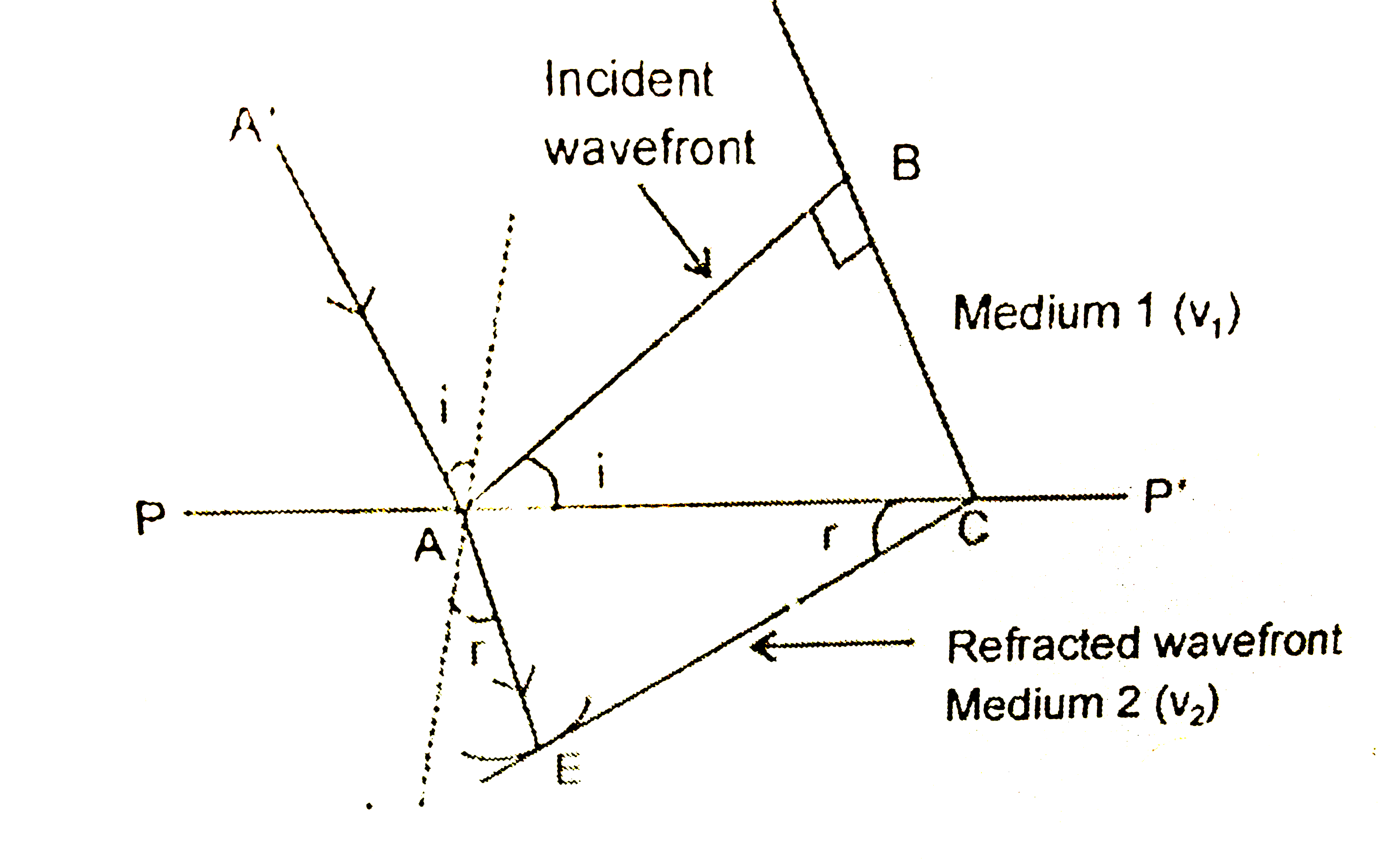 View Solution
View SolutionThe shape of reflected wavefronts in case of reflection of plane wave front from concave mirror is
View SolutionDefine the term wavefront. Using Huygens' wave theory, verify the laws of reflection.
View SolutionLigtht falls on a plane reflecting surface.For what angler of incidence is the reflected ray normal to the incident ray.
View SolutionSpherical wave fronts shown in figure,strike a plane mirror .reflected
 View Solution
View Solution

