How many times a particle will reach maximum displacement during the time taken by the wave to advance by one wavelength?
To solve the problem of how many times a particle will reach maximum displacement during the time taken by the wave to advance by one wavelength, we can follow these steps:
1. Understand the Wave Motion:
- A wave propagates through a medium, and particles of the medium oscillate around their equilibrium positions. The maximum displacement from the equilibrium position is known as the amplitude (A).
2. Identify the Wave Equation:
- The wave can be represented by the equation:
y=Asin(ωt−kx)
- Here, y is the displacement, A is the amplitude, ω is the angular frequency, k is the wave number, t is time, and x is the position.
3. Determine the Time for One Wavelength:
- The time taken for the wave to advance by one wavelength (λ) is the wave's period (T). The relationship between wavelength, frequency (f), and wave speed (v) is given by:
v=fλ
- The period T can also be expressed as:
T=1f
4. Identify Maximum Displacement Points:
- During one complete cycle of the wave (one wavelength), the particle will reach maximum displacement twice: once in the positive direction (amplitude A) and once in the negative direction (-A).
5. Conclusion:
- Therefore, during the time taken by the wave to advance by one wavelength, the particle will reach maximum displacement 2 times.
Final Answer:
The particle will reach maximum displacement 2 times during the time taken by the wave to advance by one wavelength.
---
- A wave propagates through a medium, and particles of the medium oscillate around their equilibrium positions. The maximum displacement from the equilibrium position is known as the amplitude (A).
- The wave can be represented by the equation:
y=Asin(ωt−kx)
- Here, y is the displacement, A is the amplitude, ω is the angular frequency, k is the wave number, t is time, and x is the position.
- The time taken for the wave to advance by one wavelength (λ) is the wave's period (T). The relationship between wavelength, frequency (f), and wave speed (v) is given by:
v=fλ
- The period T can also be expressed as:
T=1f
- During one complete cycle of the wave (one wavelength), the particle will reach maximum displacement twice: once in the positive direction (amplitude A) and once in the negative direction (-A).
- Therefore, during the time taken by the wave to advance by one wavelength, the particle will reach maximum displacement 2 times.
The particle will reach maximum displacement 2 times during the time taken by the wave to advance by one wavelength.
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)
59 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
13 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
An harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
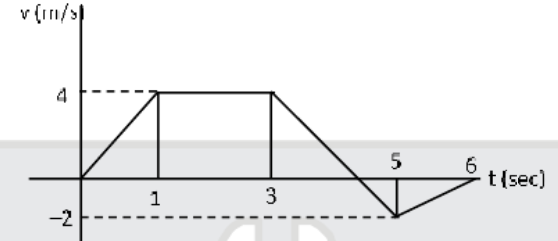
View Solution
Knowledge Check
In the question number 67, the time taken by the ball to reach the ground is
A2 sB3 sC5 sD7 sFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)
A simple harmonic progressive wave in a gas has a particle displacement of y=a at time t=T/4 at the orgin of the wave and a particle velocity of y =v at the same instant but at a distance x=λ/4 from the orgin where T and λ are the periodic time and wavelength of the wave respectively. then for this wave.
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
View SolutionFrom a tower of height H, a particle is thrown vertically up with a speed V. The time taken by the particle to hit the ground 3 tiem that taken by it to reach the highest point of is path . Then find H.
View SolutionIf time taken by the projectile to reach Q is T, than PQ=

View SolutionFor ground to ground projectile, time take by a particle to ge point O to point C is T1 and during the same motion time taken by the particle to ge from A to B is T2 then height 'h' is :

View Solution
