A given conductor has got different areas of cross section. From the formula for drift speed can we say the current i will be different at different cross sections?
To determine if the current I will be different at different cross-sections of a conductor with varying areas of cross-section, we can analyze the relationship between current, drift speed, and cross-sectional area.
1. Understanding the Formula for Current:
The current I flowing through a conductor can be expressed using the formula:
I=n⋅A⋅e⋅vd
where:
- n = number of charge carriers per unit volume,
- A = cross-sectional area,
- e = charge of an electron,
- vd = drift velocity of the charge carriers.
2. Analyzing Different Cross-Sections:
In a conductor with varying cross-sectional areas, let’s consider two different cross-sections A1 and A2. According to the formula, if the area changes, it could affect the current.
3. Effect of Area on Drift Velocity:
When the area of cross-section increases (e.g., from A1 to A2), the drift velocity vd must adjust to maintain the same current I. This is because the total current flowing through the conductor must remain constant in a steady state.
4. Relationship Between Area and Drift Velocity:
If the area increases, the drift velocity decreases. This is due to the conservation of charge flow. The product A⋅vd must remain constant for the current to remain the same:
I=n⋅A1⋅e⋅vd1=n⋅A2⋅e⋅vd2
Thus, if A1<A2, then vd1>vd2.
5. Conclusion:
Therefore, even though the area of cross-section changes, the current I remains constant throughout the conductor. This means that the current will not be different at different cross-sections, despite the changes in drift velocity.
Final Answer:
The current I remains constant at different cross-sections of the conductor, even though the drift velocity vd changes with varying cross-sectional areas.
The current I flowing through a conductor can be expressed using the formula:
I=n⋅A⋅e⋅vd
where:
- n = number of charge carriers per unit volume,
- A = cross-sectional area,
- e = charge of an electron,
- vd = drift velocity of the charge carriers.
In a conductor with varying cross-sectional areas, let’s consider two different cross-sections A1 and A2. According to the formula, if the area changes, it could affect the current.
When the area of cross-section increases (e.g., from A1 to A2), the drift velocity vd must adjust to maintain the same current I. This is because the total current flowing through the conductor must remain constant in a steady state.
If the area increases, the drift velocity decreases. This is due to the conservation of charge flow. The product A⋅vd must remain constant for the current to remain the same:
I=n⋅A1⋅e⋅vd1=n⋅A2⋅e⋅vd2
Thus, if A1<A2, then vd1>vd2.
Therefore, even though the area of cross-section changes, the current I remains constant throughout the conductor. This means that the current will not be different at different cross-sections, despite the changes in drift velocity.
The current I remains constant at different cross-sections of the conductor, even though the drift velocity vd changes with varying cross-sectional areas.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-1)
17 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
A conductor-carries a current of 50μA If the area of cross-section of the conductor is 50mm2, then value of the current density in Am−2
View SolutionA charge 0.5C passes through a cross section of a conductor in 5s. Find the current.
View SolutionIf n,e,A and vd are free electron density inside conductor , charge of electron , area of cross-section of conductor and drift velocity of free electrons inside conductor, then current l through the conductor is
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionAssertion : If a current is flowing through a conducting wire of non-uniform cross-section, drift speed and resistance both will increase at a section where cross-sectional area is less.
Reason : Current density at such sections is more where cross-sectional area is less.
View SolutionThe length of a current-carrying cylindrical conductor is l, its area of cross-section is A, the number density of free electrons in it is n, and the drift velocity of electrons in it is vd . The number of electrons passing through a particular cross-section of the conductor per unit time is given by:
View SolutionIn a photoelectric experiment under conditions of saturation current , we consider two different cross - section A and B as shown. Here , vAandvB represent the average speed of electrons at the two cross - sections .
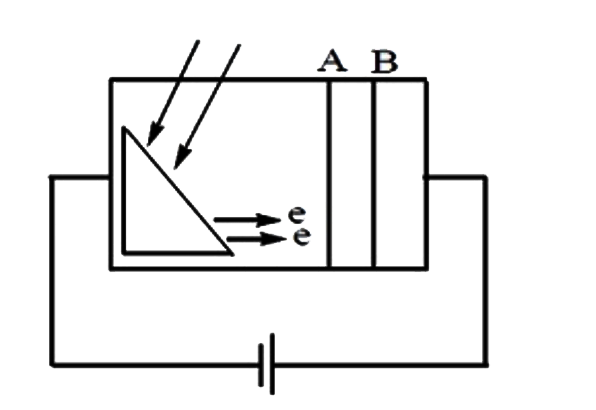
View SolutionConsider a conductor of variable cross section in which current is flowing from cross section 1 to 2. Then
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
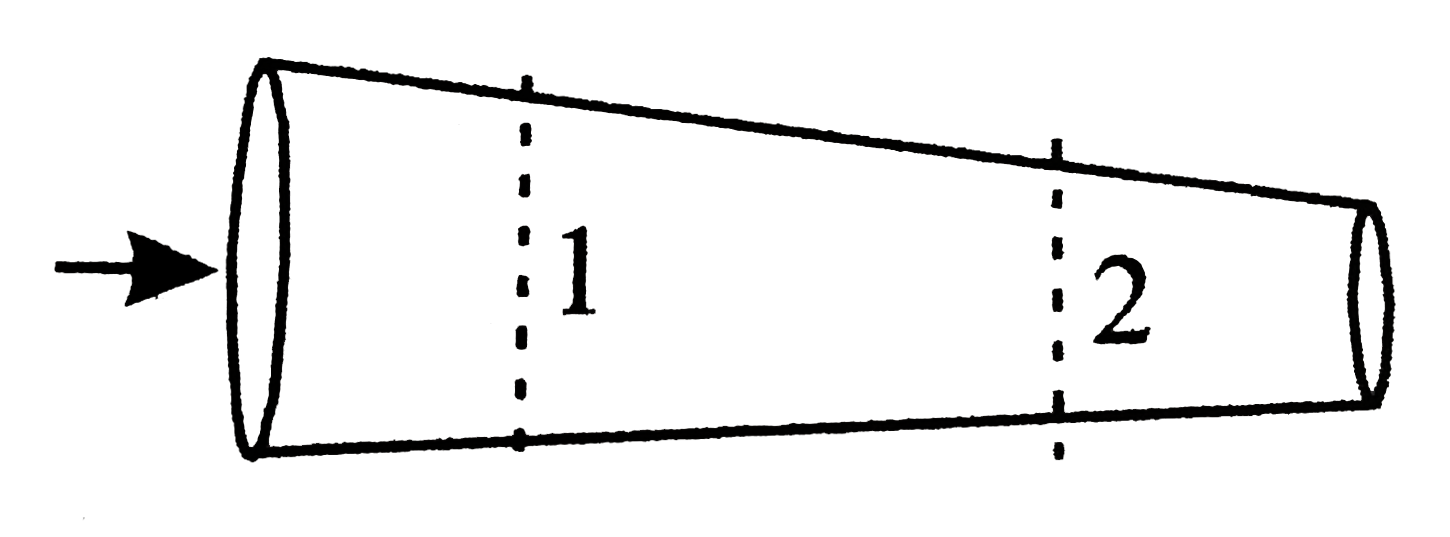
View SolutionA conical section of a pipe is shown in figure through which water is flowing. Let A be the area of crosss-section, r be the radius of cross-section, P be the pressure at a point difference and v be the velocity of water.

Match the column-I with column-II containing values of ratio of quantities given in Column-I
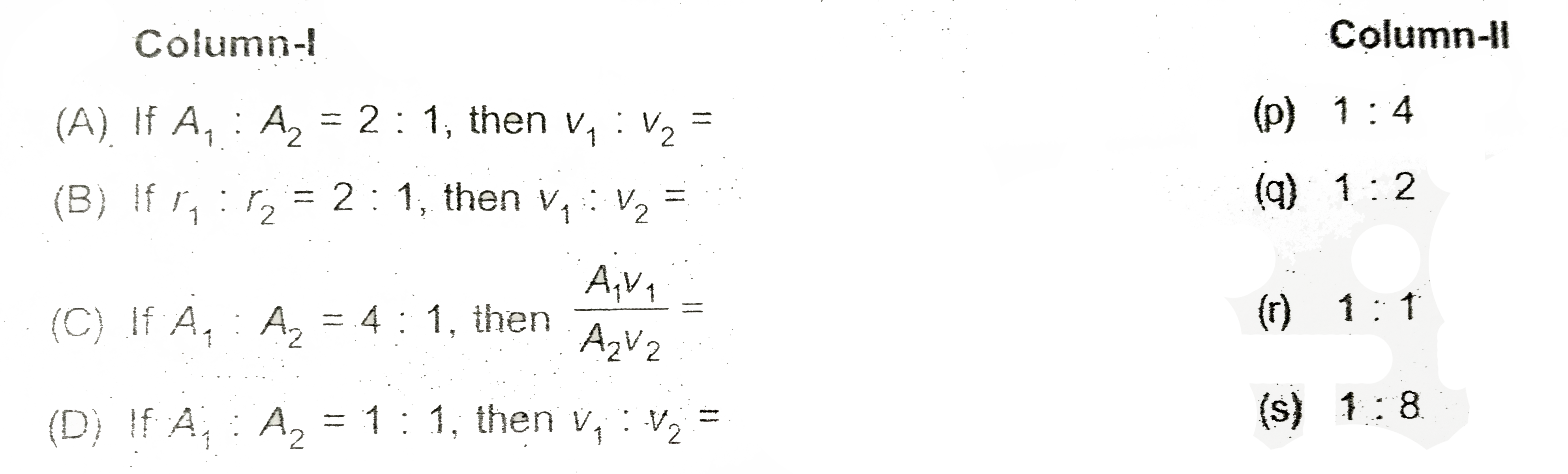
View Solution
