When is the series combination of cells advantageous and why?
Step-by-Step Solution:
1. Understanding Series Combination of Cells:
- A series combination of cells involves connecting multiple cells end-to-end, so that the positive terminal of one cell is connected to the negative terminal of the next cell.
2. When is it Advantageous?:
- The series combination of cells is advantageous when a high potential difference (or high electromotive force, EMF) is required for a circuit.
3. Reason for High Potential:
- In a series combination, the total potential difference across the combination is the sum of the individual potentials of each cell. If each cell has a potential difference of V, and there are n cells connected in series, the total potential difference Vtotal is given by:
Vtotal=n×V
- This means that if you need a higher voltage for your application, you can achieve that by adding more cells in series.
4. Application of Kirchhoff's Voltage Law:
- According to Kirchhoff's voltage law, the sum of the potential differences (voltage) around any closed loop in a circuit must equal zero. Therefore, in a series circuit, the total voltage is the sum of the voltages across each cell.
5. Conclusion:
- Thus, the series combination of cells is particularly advantageous in situations where a high voltage is necessary, such as in powering devices that require more energy to operate.
- A series combination of cells involves connecting multiple cells end-to-end, so that the positive terminal of one cell is connected to the negative terminal of the next cell.
- The series combination of cells is advantageous when a high potential difference (or high electromotive force, EMF) is required for a circuit.
- In a series combination, the total potential difference across the combination is the sum of the individual potentials of each cell. If each cell has a potential difference of V, and there are n cells connected in series, the total potential difference Vtotal is given by:
Vtotal=n×V
- This means that if you need a higher voltage for your application, you can achieve that by adding more cells in series.
- According to Kirchhoff's voltage law, the sum of the potential differences (voltage) around any closed loop in a circuit must equal zero. Therefore, in a series circuit, the total voltage is the sum of the voltages across each cell.
- Thus, the series combination of cells is particularly advantageous in situations where a high voltage is necessary, such as in powering devices that require more energy to operate.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS) (Choose the correct alternative)3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-1)17videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)12videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)16videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
In series combination of resistances :
Ap.d. is same across each resistanceBtotal resistance is reducedCcurrent is same in each resistanceDall above are true. - Question 2 - Select One
In the series combination of n cells each cell having emf ε and internal resistance r. If three cells are wrongly connected, then total emf and internal resistance of this combination will be
Anε,(nr−3r)B(nε−2r),nrC(nε−4ε),nrD(nε−6ε),nr - Question 3 - Select One
In parallel combination of n cells, we obtain
Amore voltageBmore currentCless voltageDless current
When a battery is connected across a series combination of self inductance L and resistance R , the variation in the current i with time t is best represented by
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe V - I graphs for two resistors and their series combination are shown in Fig 5.23. Which one of these graphs represents the series combination of the two resistors? Given reason for your answer.
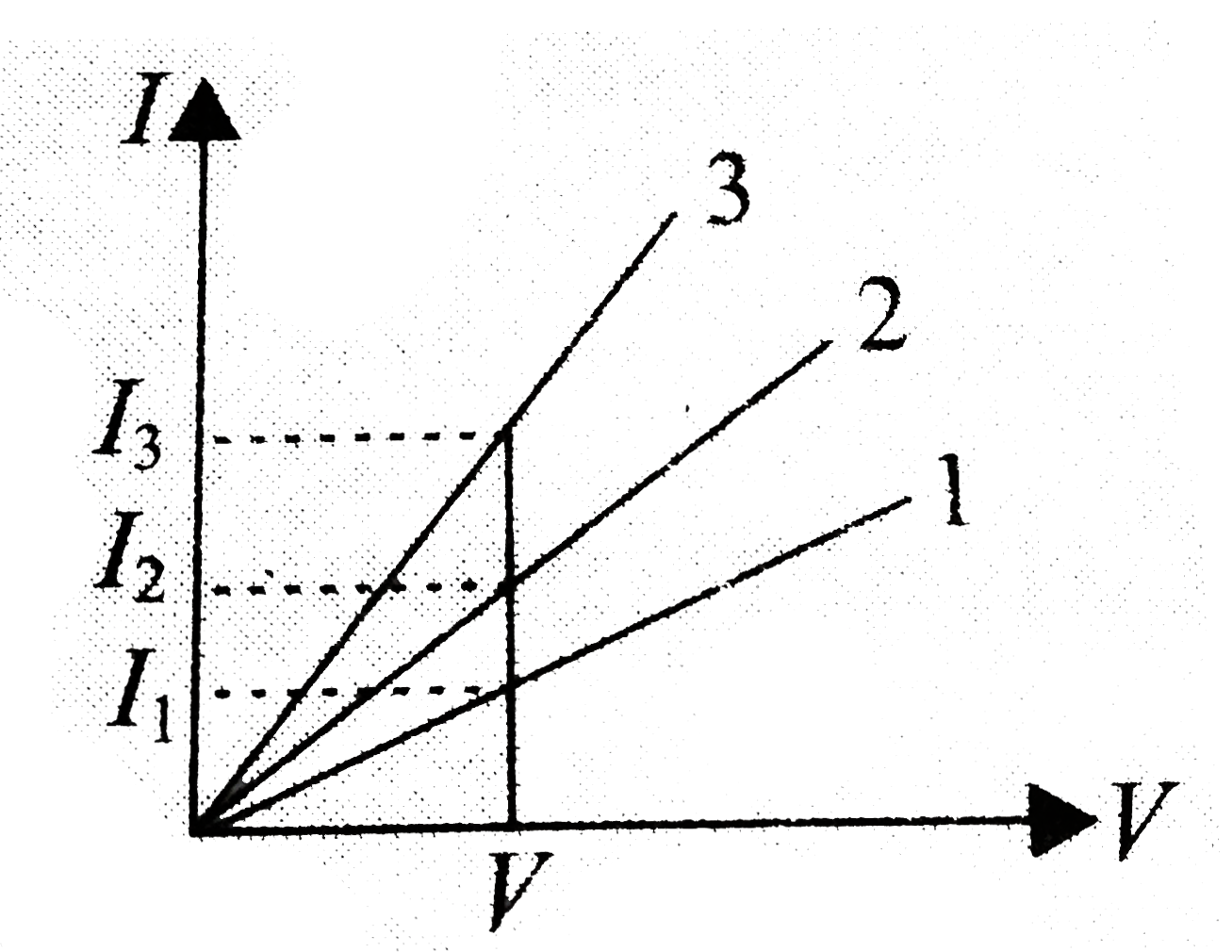 View Solution
View SolutionIn the series combination of two or more than two resistances
View Solution