Find the equivalent resistance of the circuit of the previous problem between the ends of an edge such as a and b in figure.
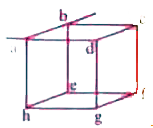
Suppose a current i enters the circuit at the point a and the same current leaves the circuit at the point b. The current distribution is shown is figure.
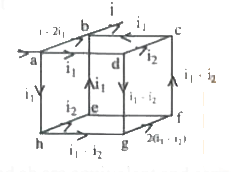
The paths through .ad. and ah are equivalent and carry equal current i1. The current through ab is then i−2i1.
The same distribution holds at the junction b. Currents in eb and cb are i1 each. The current i1 in ah is divided into a part i2 in he and i1−i2 in hg. Similar is the division of current i1 in ad into dc and dg. The rest of the currents may be written easily using Kirchhoff.s junction law. The potential difference V between a and b may be written from the paths ab, aheb and ahgfcb as
V=(i−2i1)r,V=(i1+i2+i1)r
and V=[i1+(i1−i2)+2(i1−i2+i(i1−i2)+i1]r
Which may be written as
V=(i−2i1)r,V=(2i1+i2)randV=(6i1−4i2)r
Eliminating i1andi2 from these equations,
Vi=712r
∴ The equivalent resistance =7r/12
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Linked Comprehension Type Questions))
9 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Find the equivalent resistance of the circuit of the previous problen between the ends of an edge such as a and b in figure.

View SolutionFind the equivalent resistance of the circuit of the previous problen between the ends of an edge such as a and b in figure.

View SolutionFind the equivalent resistance of the circuit between A and B

View SolutionFind the equivalent resistance of the circuit between the points A and B

View SolutionCalculate the equivalent resistance of the circuit shown in figure between the points a and b.
View SolutionFind equivalent resistance of the circuit between the terminals A and B.
View SolutionFind equivalent resistance of the circuit between the terminals A and B.
View SolutionFind the equivalent resistance of the circuit shown in figure between the points a and b.Each resistor has a resistances r.

View SolutionFind the equivalent resistance of the circuit shown in figure between the points a and b.Each resistor has a resistances r.

View SolutionFind the equivalent resistance of the circuits shown in figure between the points a and b. Each resistor has a resistance r.


View Solution
