Parallel sides of a trapezium are 14 cm and 35 cm and the area is 1176 cm2. What is the value of the distance (in cm) between parallel sides?
72
96
24
48
The correct Answer is:D
To find the distance between the parallel sides of the trapezium, we can use the formula for the area of a trapezium:
Area=12×(L1+L2)×h
Where:
- L1 and L2 are the lengths of the parallel sides,
- h is the height (the distance between the parallel sides).
Given:
- L1=14cm
- L2=35cm
- Area = 1176cm2
Step 1: Substitute the values into the area formula.
1176=12×(14+35)×h
Step 2: Calculate L1+L2.
L1+L2=14+35=49
Step 3: Substitute this sum back into the area formula.
1176=12×49×h
Step 4: Multiply both sides by 2 to eliminate the fraction.
2352=49×h
Step 5: Solve for h by dividing both sides by 49.
h=235249
Step 6: Perform the division.
h=48cm
Thus, the distance between the parallel sides of the trapezium is 48cm.
- L1 and L2 are the lengths of the parallel sides,
- h is the height (the distance between the parallel sides).
- L1=14cm
- L2=35cm
- Area = 1176cm2
Similar Questions
Parallel sides of a trapezium are 26 cm and 40 cm and the area is 792cm2. What is the value of the distacne (in cm) between parallel sides ?
View SolutionParallel sides of a trapezium are 26 cm and 40 cm and the area is 792cm2. What is the value of the distacne (in cm) between parallel sides ?
View Solution
Knowledge Check
If the lengths of the two parallel sides of a trapezium are 4 cm and 6 cm. and its area is 25cm2. Find the distance between its parallel sides (in cm.).
A2.5B10C5D7.5If the lengths of the two parallel sides of a trapezium are 4 cm and 6 cm. and its area is 25cm2. Find the distance between its parallel sides (in cm.).
A2.5B10C5D7.5If the lengths of the two parallel sides of a trapezium are 8 cm and 10 cm. and its area is 54cm2. Find the distance between its parallel sides (in cm.).
A6B3C12D9
If the length of the parallel sides of an isosceles trapezium are 20 cm and 30 cm and the area is 100 cm2, then what is the length of the non-parallel sides ?
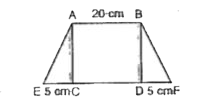
View SolutionIf the lengths of the two parallel sides of a trapezium is 5 cm and 7 cm and its area is 24 cm2. Find the distance between its parallel sides (in cm).
View SolutionThe lengths of the parallel sides of a trapezium are 19 cm and 13 cm and its area is 128cm2. The distance between the parallel sides is
View SolutionThe lengths of parallel sides of a trapezium are 19 cm and 13 cm and its area is 128cm2 . The distance between the parallel sides is:
View SolutionThe parallel sides of a trapezium are 54 cm and 26 cm and the distance between them is 15 cm. The area of the trapezium is
View Solution
