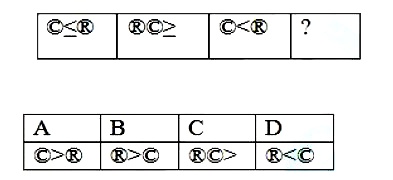
What will come in the place of question (?) mark in following number series:
104, ?, 96, 120, 88, 128
112
110
114
118
The correct Answer is:A
To solve the problem of finding the missing number in the series 104,?,96,120,88,128, we will analyze the pattern in the series step by step.
Step 1: Write down the series
We have the series:
- 104, ?, 96, 120, 88, 128
Step 2: Identify the known numbers
The known numbers in the series are:
- 104 (1st term)
- ? (2nd term)
- 96 (3rd term)
- 120 (4th term)
- 88 (5th term)
- 128 (6th term)
Step 3: Analyze the differences between the known terms
Let's look at the differences between the consecutive known terms:
- From 104 to 96: 104−96=8 (decrease)
- From 96 to 120: 120−96=24 (increase)
- From 120 to 88: 120−88=32 (decrease)
- From 88 to 128: 128−88=40 (increase)
Step 4: Identify the pattern in the differences
The differences we calculated are:
- Decrease of 8
- Increase of 24
- Decrease of 32
- Increase of 40
Now, let's look at the pattern of the differences:
- The decreases are: 8, 32 (difference of 24)
- The increases are: 24, 40 (difference of 16)
Step 5: Find the missing term
Now, we need to find the missing term (2nd term). We can assume that the pattern alternates between a decrease and an increase.
If we denote the missing term as x:
- The difference from 104 to x should be a decrease (let's denote it as d1).
- The difference from x to 96 should be an increase (let's denote it as d2).
From our earlier analysis, we can see that:
- If we assume d1=16 (a decrease), then:
x=104−16=88
- If we assume d2=8 (an increase), then:
96=x+8⟹x=96−8=88
Conclusion
The missing number in the series is 112.
Final Answer
The answer is 112.
---
We have the series:
- 104, ?, 96, 120, 88, 128
The known numbers in the series are:
- 104 (1st term)
- ? (2nd term)
- 96 (3rd term)
- 120 (4th term)
- 88 (5th term)
- 128 (6th term)
Let's look at the differences between the consecutive known terms:
- From 104 to 96: 104−96=8 (decrease)
- From 96 to 120: 120−96=24 (increase)
- From 120 to 88: 120−88=32 (decrease)
- From 88 to 128: 128−88=40 (increase)
The differences we calculated are:
- Decrease of 8
- Increase of 24
- Decrease of 32
- Increase of 40
- The decreases are: 8, 32 (difference of 24)
- The increases are: 24, 40 (difference of 16)
Now, we need to find the missing term (2nd term). We can assume that the pattern alternates between a decrease and an increase.
- The difference from 104 to x should be a decrease (let's denote it as d1).
- The difference from x to 96 should be an increase (let's denote it as d2).
- If we assume d1=16 (a decrease), then:
x=104−16=88
96=x+8⟹x=96−8=88
The missing number in the series is 112.
The answer is 112.
Topper's Solved these Questions
- BOOK - ADDA247CHAPTER - NUMBER SERIESEXERCISE - MAINS QUESTIONS30videos
NUMBER SERIES
- BOOK - ADDA247CHAPTER - MIXTURE & ALLIGATIONEXERCISE - PREVIOUS YEAR QUESTIONS21videos
MIXTURE & ALLIGATION
- BOOK - ADDA247CHAPTER - NUMBER SYSTEM, SIMPLIFICATION AND APPROXIMATION EXERCISE - PREVIOUS YEAR QUESTION60videos
NUMBER SYSTEM, SIMPLIFICATION AND APPROXIMATION
Similar Questions
Knowledge Check
- Question 1 - Select One
What will come in place of question mark(?) in the following number series?
7 8 15 46 ? 916A185B182C181D183 - Question 2 - Select One
What will come in place of question mark (?) inthe following number series'
23 32 45 62 83 ?A116B106C102DNone of the above - Question 3 - Select One
What will come in place of question mark (?) in the following number series'
9 20 42 75 119 ?A174B170C168D180
What will come in place of question mark (?) inthe following number series'
17 23 35 59 107 ?View SolutionWhat will come in place of question mark(?) in the following number series?
33 636 ? 103680View SolutionWhat will come in place of question mark(?) in the following number series?
5, 9 ,25, 61 ,125 ?View SolutionWhat will come in place of question mark (? ) in the following number series ?
27 38 71 126 203 ?View SolutionWhat will come in the place of question mark (?) in the below series?
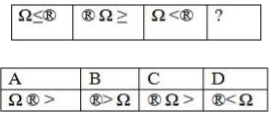 View Solution
View Solution