The molar entropies of HI(g),H(g)andI(g) at 298K are 206.5, 114.6, and 180.7Jmol−1K−1 respectively. Using the ΔG∘ given below, calculate the bond energy of HI.
HI(g)→H(g)+I(g),ΔG∘=271.8kJ (Give your answer after divide with 49.7)Solution in Telugu
282.4kJmol−1
298.3kJmol−1
290.1kJmol−1
315.4kJmol−1
The correct Answer is:B
ΔS∘=−206.5+114.6+180.7=88.8
ΔG∘=ΔH∘−TΔS∘
ΔH∘=271.8+298×88.8×10−3
ΔH∘=298.3
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.121 To Q.150)1videos
THERMODYNAMICS
- BOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 2 (Q.1 To Q.30)1videos
THERMODYNAMICS
- BOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.31 To Q.60)2videos
THERMODYNAMICS
- BOOK - NARENDRA AWASTHICHAPTER - STOICHIOMETRYEXERCISE - Level 3 - Subjective Problems20videos
STOICHIOMETRY
Similar Questions
Gasoline has an enthalpy of combustion 24000 kJ/mol gallon. When gasoline burns in an automobile engine, approximately 30% of the energy released is used to produce mechanical work. The remainder is lost as heat transfer to the engine's cooling system. As a start on estimating how much heat transfer is required, calculate what mass of water could be heated from 25∘C to 75∘C by the combustion of 1.0 gallon of gasoline in an automobile? (Given : C(H2O)=4.18J/g∘C)
02:06View SolutionTwo moles of a triatomic linear gas (neglect vibration degree of freedom) are taken through a reversible process ideal starting from A as shown in figure.
The volume ratio VBVA=4. If the temperature at A is −73∘C, then :
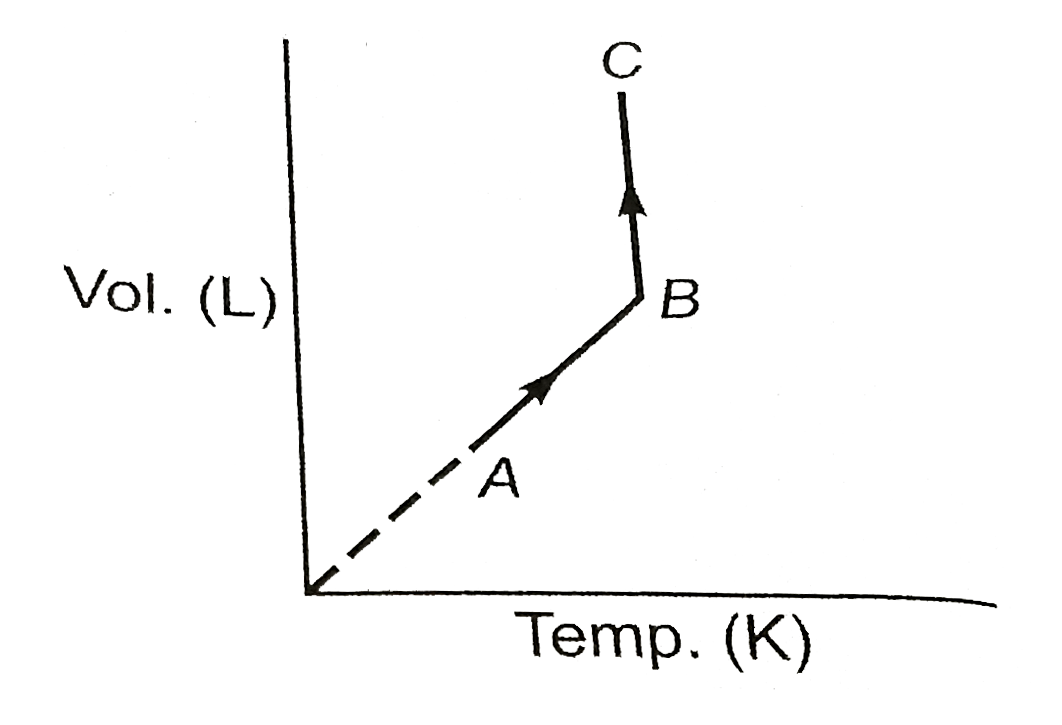
(ii) Total enthalpy change in both steps is :04:07View SolutionA gas expands against a variable pressure given by P=20V (where P in atm and V in L). During expansion from volume of 1 litre to 10 litre, the gas undergoes a change in internal energy of 400 J. How much heat is absorbed by the gas during expansion?
View SolutionWhat volume of a liquid (in L) will contain 10 mole ? If molar mass of liquid is 280 and its density is 1.4 g/mL.
01:42View SolutionFor the reaction, 2NO_(g) + O_(2)(g) rarr 2NO_(2)(g) Calculate DeltaG at 700K when enthalpy and entropy changes are -113.0 kJ mol^(-1) and -145 J K^(-1) mol^(-1) , respectively.
01:08View SolutionThe entropies of H_(2) (g) and H (g) are 130.6 and 114.6 J mol^(-1)K^(-1) respectively at 298 K. Using the data given below calculate the bond energy of H_(2) (in kJ/mol) : H_(2)(g)rarr2H(g),DeltaG^(@)=406.6kJ
02:57View SolutionThe molar entropies of HI(g), H(g) and I(g) at 298 K are 206.5, 114.6, and 180.7 J mol^(-1)K^(-1) respectively. Using the DeltaG^(@) given below, calculate the bond energy of HI. HI(g)rarrH(g)+I(g)," "DeltaG^(@)=271.8 kJ
04:14View SolutionThe entropies of H2(g) and H(g) are 130.6 and 114.6Jmol−1K−1 respectively at 298 K. Using the data given below calculate ΔH∘ ( in kJ/ mol) of the reaction given below.
H2(g)→2H(g) , ΔG∘=406.62kJ/mol05:05View SolutionThe entropies of H_(2)(g) and H(g) are 60 " and " 50 J"mole"^(-1)K^(-1) respectively at 300 K. Using the data given below calcualate the bond enthalpy of H_(2)(g) in Kcal "mole"^(-1) . " "H_(2)(g) rarr 2H(g)," "DeltaG^(@)=21.6 KJ "mole"^(-1)
04:39View SolutionDeltaG^(@)(HI,g)-=+1.7kJ. What is the equilibrium constnt at 25^(@)C"for"2 HI_((g))hArrH_(2(g))+I_(2(g))
02:51View Solutionयदि अभिक्रिया H2(g)+I2(g)⇔2HI(g) के लिए K का मान 48 ह तब अभिक्रिया 12H2(g)+12I2⇔HIg के लिए K का मान क्या होगा ?
01:10View Solutionwill the reaction, I_(2_((g)))+H_(2)S_((g))rarr2HI_((g))+S_((s)) proceed spontaneously in the forward direction at 298K ? You are given with DeltaG^(@) for HI and H_(2) as 1.8 and -33.8 kJ mol^(-1) respectively . Given : I_(2_((g)))+H_(2)S_((g))rarr2HI_((g))+S_((s)) DeltaG_(HI)^(@)=1.8kJ mol^(-1) DeltaG_(H_(2)S)^(@)=1.8kJ mol^(-1)
01:43View SolutionCalculate the standard free energy change (ΔG∘) of the following reaction and say whether it is feasible at 373 K or not 12H2(g)+12I2(g)→HI(g),ΔH∘ris + 25.95 kJ mole−1. Standard entropies of HI(g).H2(g)andI2(g) are 206.3, 130.6 and 116.7JK−1mole−1.
02:59View SolutionThe molar entropies of HI(g),H(g)andI(g) at 298K are 206.5, 114.6, and 180.7Jmol−1K−1 respectively. Using the ΔG∘ given below, calculate the bond energy of HI.
HI(g)→H(g)+I(g),ΔG∘=271.8kJ (Give your answer after divide with 49.7)04:00View SolutionH_(2(g)) reacts with I_(2(g)) to give HI_((g)) . Write the rate equation and predict order.
03:07View SolutionH2(g) reacts with I2(g) to give HI(g). Write the rate equation and predict order of the reaction with respect to H2 and I2.
01:22View Solution

