A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec Solution in Telugu
The correct Answer is:6
Step by step video, text & image solution for A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s= f(t)=8t+t^3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MATHEMATICS -II(B) MODEL PAPER -10EXERCISE - SECTION-C9videos
MATHEMATICS -II(B) MODEL PAPER -10
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MATHEMATICS -II(B) MODEL PAPER -10EXERCISE - SECTION-C9videos
MATHEMATICS -II(B) MODEL PAPER -10
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MATHEMATICS -I(B) MODEL PAPER -9EXERCISE - SECTION-C7videos
MATHEMATICS -I(B) MODEL PAPER -9
- BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER - 7EXERCISE - Section - C (Long Answer Type Questions)7videos
MODEL PAPER - 7
Similar Questions
Find the orthocentre of the triangle formed by the vertices (-2,-1),(6,-1),(2,5)
03:42View SolutionFind the orthocentre of the triangle formed by the vertices (-2,-1),(6,-1),(2,5)
05:02View SolutionFind the orthocentre of the triagle whose vertices are (−2,−1)(6,−1),(2,5).
03:30View SolutionFind the circumcentre of the triangle whose vertices are (1,3) (0,-2) and (-3,1).
01:42View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
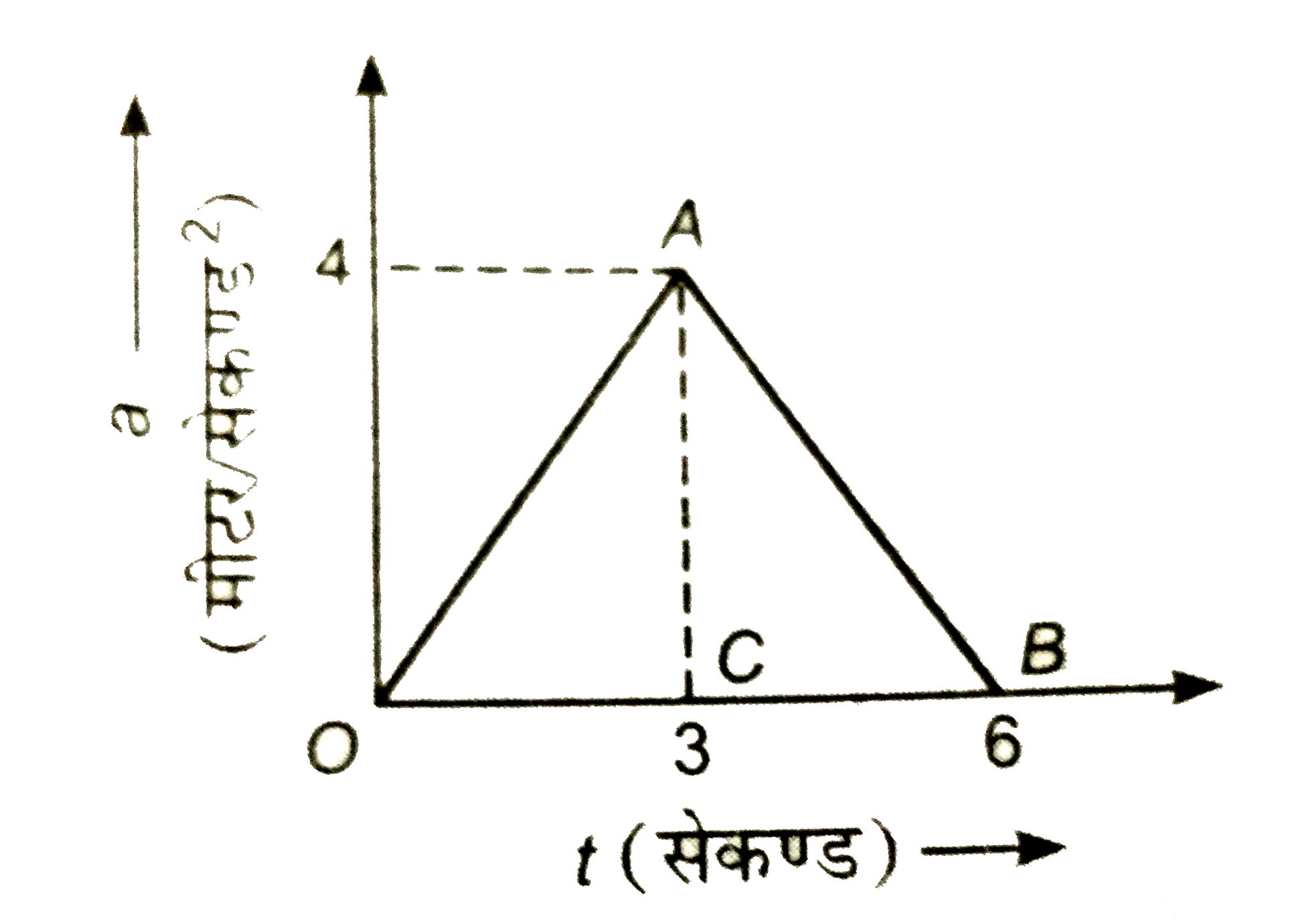
04:33View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
 04:10View Solution
04:10View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
03:55View Solutionएक कण एक सरल रेखा में इस तरह से चलता हैं ताकि इसका स्थिति t सेकेण्ड के बाद s(t)=6t−t2 हैं | इसका प्रारंभिक वेग क्या हैं।
02:35View SolutionA particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec02:35View SolutionA particle is moving in a straight line and its distance x cm from a fixed point on the line at any time t seconds is given by ,
x=112t4−23t3+32t2+t+15.
At what time is the velocity minimum ? Also find the minimum velocity.04:06View SolutionAt time t, the distance s of a particle moving in a straight line is given by s=4t2+2t. Find the average velocity between t= 2sec and t= 8 sec.
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
01:51View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
02:54View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
04:33View SolutionA particle is moving in a straight line is at a distance S from a point O on the line in time t, where S=t3−6t2+8t+5.Find the velocity when the acceleration is 12cm/sec2.
01:51View SolutionA particle is moving along a line according s= f(t) = 8t + t^3 . Find the initial velocity
04:33View Solution

