Question

State and prove the law of conservation of energy in case of a freely falling body. A machine-gun fires 360 bullets per minute and each bullet travels with a velocity of 600m/s. Of the mass of each bullet is 5 gm, find the power of the machine-gun.

Explanation

Law of conservation of energy: When forces doing work on a system are conservative then total energy of the system is constant i.e. energy can neither be created nor destroyed. Explanation : When conservative forces are applied on a system then the total mechanical energy is
(1) as kinetic energy which depends on motion OR
(2) as potential energy which depends on position of the body. So for an isolated system, energy may be transformed from one form to another but total energy is constant i.e. energy can neither be created nor destroyed.
Proof: In case of a freely falling body: Let a body of mass is dropped from a height .H. at point A. Forces due to gravitational field are conservative forces. so total mechanical energy (E=P.E + K.E.) is constant i.e., neither destroyed nor created.

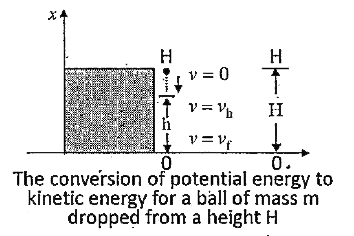
1. At point H: Velocity of body v=0
`therefore K_(H) = (1)/(2) mv^(2)= 0`
Potential energy `v(h)= mgH`
where h= height above the ground
`T.E= v(h) + K_(H)= mgH` ...(1)
2. At point i.e., just before touching the ground:
A constant force is a special case of specially dependent force F(x) so mechanical energy is conserved. So energy at H = Energy at 0 = mgH
Proof: At point .O. height `h= 0 rArr v(h)= mgH= 0`
`K_(0)= (1)/(2) mv^(2)= (1)/(2) m2gH= mgH`
Total energy E =`mgH + 0= mgH` ........ (2).
3. At any point h: `v(h)= mgh, K_(h)= (1)/(2) mv^(2)` Let height above ground = h
`v(h)= mgh, K_(h)= (1)/(2) mV^(2)` where `V= sqrt(2g(h-x))`
`therefore` Velocity of the body when it falls through a height `(h – x)` is `sqrt(2g(h-x))`
`therefore` Total energy = `mgh+ (1)/(2) m2 g(H-h)`
`rArr E= mgH+ mgH - mgh= mgH`...... (3)
From eq. 1, 2 & 3 total energy at any point is constant. Hence law of conservation of energy is proved.
Conditions to apply law of conservation of energy :
(1) Work done by internal forces is conservative.
(2) No work is done by external force. When the above two conditions are satisfied then total mechanical energy of a system will remain constant.
Problem : Number of bullets, n = 360
Time t = 1 minute = 60s
Velocity of the bullet, `v = 600ms^(-1)`
Mass of each bullet `m=5gm = 5 xx 10^(-3)kg`
Power of the machine gun,
`P= (n((1)/(2) mv^(2)))/(t)= (360 ((1)/(2) xx 5 xx 10^(-3) xx (600)^(2)))/(60)`
`rArr P= 5400W= 5.4kW`