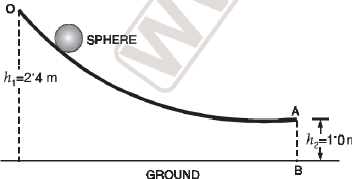
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground level and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown in fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass?
 Solution in Punjabi
Solution in Punjabi
Step by step video & image solution for A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground level and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown in fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Moment of InertiaBOOK - MODERN PUBLICATIONCHAPTER - Moment of InertiaEXERCISE - Example
323 Videos
- Gravitational potential and potential energyBOOK - MODERN PUBLICATIONCHAPTER - Gravitational potential and potential energyEXERCISE - Exercise
17 Videos
- Motion of SatellitesBOOK - MODERN PUBLICATIONCHAPTER - Motion of SatellitesEXERCISE - Exercise
25 Videos
Similar Questions
The moment of inertia of a thin rod about an axis passing through its centre and perpendicular to its length is 1,200gcm2. If length of the rod is 20 cm, find its moment of inertia about an axis passing through its one end and perpendicular to its length.
View SolutionWhat do you understand by gravitational field?
View SolutionDefine orbital velocity of a satellite. Obtain an expression for orbital velocity of a satellite.
View SolutionFigure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?
View SolutionA small sphereical ball is released from a point at a height h on a rough track shown in figure. Assuming that it dow not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B ( which is vetically below the end A of the track as shown in fig.) where the sphere lands. . (A) 1 m (B) 2 m ( C) 3 m (D) 4 m .
View Solution
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View SolutionA disc of radius r = 0.1 m is rolled from a point A on a track as shown in the figure. The part AB of the track is a semi-circle of radius R in a vertical plane. The disc rolls without sliding and leaves contact with the track at its highest point B. Flying through the air it strikes the ground at point C. The velocity of the center of mass of the disc makes an angle of 30^(@) below the horizontal at the time of striking the ground. At the same instant, velocity of the topmost point P of the disc is found to be 6 m//s (Take g = 10 m//s^(2) ). (a) Find the value of R. (b) Find the velocity of the center of mass of the disc when it strikes the ground. (c) Find distance AC.
View SolutionAOB is a frictionless parabolic track in vertical plane. The equation of parabolic track can be expressed as y = (3)/(2H) x^(2) for co-ordinate system shown in the figure. The end B of the track lies at y = (H)/(2) . When a uniform small ring is released on the track at A it was found to attain a maximum height of h_(1) , above the ground after leaving the track at B. There is another track DEF which is in form of an arc of a circle of radius H subtending an angle an angle of 150^(@) at the centre. The radius of the track at D is horizontal. The same ring is released on this track at point D and it rolls without sliding. The ring leaves the track at F and attains a maximum height of h_(2) above the ground. Find the ratio (h_(1))/(h_(2)) .
View SolutionFigure shows a loop track whose lower part ends into a circular track of radius R and centre O.
A small solid sphere of mass M rolls without slipping along the loop track from the end A at a height 6R from the bottom of the track. What is the horizontal force acting on the sphere, when it rises up to the point P in level with the centre O of the circular part ?

View SolutionA small sphere rolls from the top of a sloping curved plane without slipping. The end of the plane is horizontal which is 1.0 m above the ground level and the top of the plane is 2.6 m above the ground. With respect to the point B on the ground (which is just below the point A at the end of the plane), find the distance where the sphere falls. Does the sphere continue to rotate about its center of mass during the projectile motion? explain.
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 , above the horizontal surface, the distance it will move on the rough surface is x meter. Then value of x.

View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed v0. Calculate the angle θ with respect o the vertical where it leaves contact with the track.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View Solution
