let 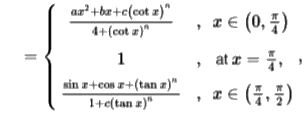where a, b, c are real constants and $f (x) = lim n \to \infty g (x) .$ If
$lim x \to \frac{π}{4}$ f(x) exists, then c may be $x \to \frac{π}{4}$ equal to

$\frac{1}{2}$

-1

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Let $g (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} \frac{a x^{2} + b x + c {(cot x)}^{n}}{4 + {(cot x)}^{n}} & , x \in (0, \frac{π}{4}) 1 & , at x = \frac{π}{4} \frac{sin x + cos x + {(tan x)}^{n}}{1 + c {(tan x)}^{n}} & , x \in (\frac{π}{4}, \frac{π}{2}) \end{matrix}$
where a, b, care real constants and $f (x) = lim n \to \infty g (x)$ If $lim x \to \frac{π}{4}$ f(x) exist then c may be equal to
A2
B $\frac{1}{2}$
C3
D $- 1$
Let $f (x) = a + b | x | + c {| x |}^{2}$ , where a,b,c are real constants. The, f'(0) exists if
Ab=0
Bc=0
Ca=0
Db=c
Let $f (x) = a {| x |}^{2} + b | x | + c$ where a,b,c are real constants. Then f'(x) exists at x=0 if:
Aa=0
Bb=0
Cc=0
Da=b