From a uniform disc of radius R, a small disc of radius R2 is cut and removed as shown in the diagram. Find the center of mass of the remaining portion of the disc.
Let us consider the mass of the uncut full disc be M. Its center of mass would be at the geometric center of the disc on which the origin coincides.
Let the mass of the small disc cut and removed be m and its center of mass is at a position R2 to the right of the origin as shown in the figure.

Hence, the remaining portion of the disc should have its center of mass to the left of the origin, say, at a distance x. We can write from the principle of moments,
(M−m)x=(m)R2
x=(m(M−m))R2
If σ is the surface mass density (i.e. mass per unit surface area), σ=MπR2 , then, the mass m of small disc is,
m surface mass density × surface area
m=σ×π(R2)2
m=(MπR2)π(R2)2=MπR2πR24=M4
substituting m in the expression for x
x=M4(M−M4)×R2=M4(3M4)×R2
x=R6
The center of mass of the remaining portion is at a distance R6 to the left from the center of the disc.
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES Book:NCERT TAMILChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES Exercise:EXERCISE (I. MULTI CHOICE QUESTION)
Explore 15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES Book:NCERT TAMILChapter:MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES Exercise:EXERCISE (V. NUMERICAL PROBLEMS)
Explore 6 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT TAMILChapter:MOTION IN A STRAIGHT LINEExercise:ADDITIONAL EXERCISES
Explore 5 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBook:NCERT TAMILChapter:NATURE OF PHYSICAL WORLD AND MEASUREMENTExercise:EXERCISE (V. Conceptual Questions)
Explore 5 Videos
Similar Questions
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
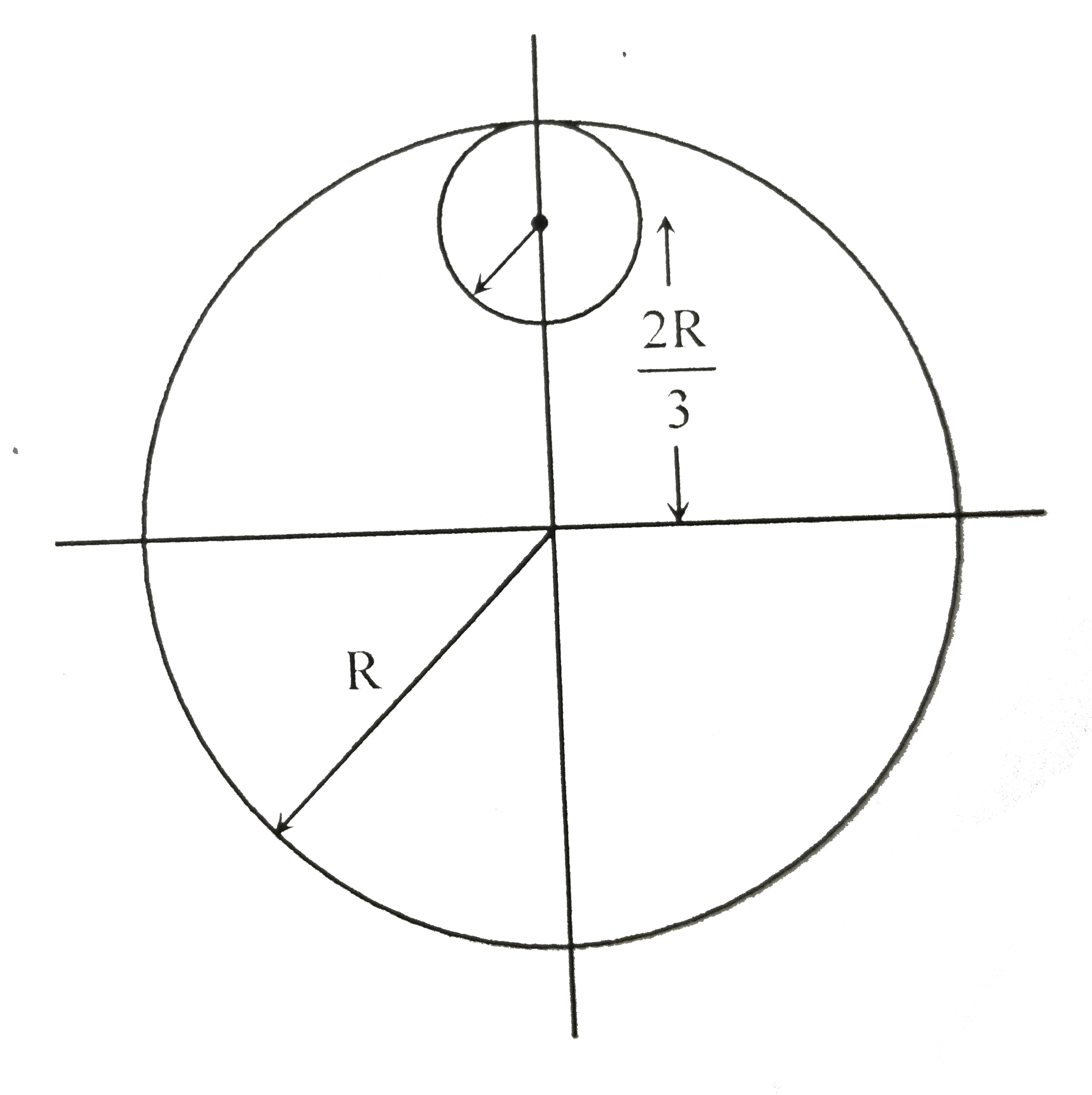 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 A4M2B409MR2C10MR2D379MR2
A4M2B409MR2C10MR2D379MR2
A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
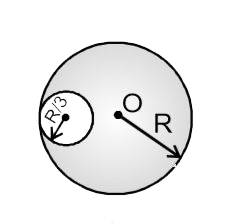
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA uniform metal disc of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
View Solution
