A projectile of mass 5 kg, in its course of motion explodes on its own into two fragments. One fragment of mass 3 kg falls at three fourth of the range R of the projectile. Where will the other fragment fall?
It is an explosion of its own without any external influence. After the explosion, the center of mass of the projectile will continue to complete the parabolic path even though the fragments are not following the same parabolic path. After the fragments have fallen on the ground, the center of mass rests at a distance R (the range) from the point of projection as shown in the diagram.
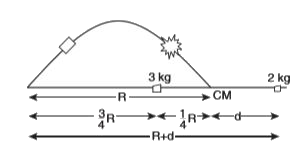
If the origin is fixed to the final position of the center of mass, the principle of moments holds good.
m1x1=m2x2
where, m1=3 kg, m2=2 kg, x1=14R. The value of x2=d
3×13R=2×d,
d=38R
The distance between the point of launching and the position of 2 kg mass is R+d.
R+d=R+38R=118R=1.375R
The other fragment falls at a distance of 1.375R from the point of launching. (Here R is the range of the projectile.)
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES BOOK - NCERT TAMILCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES EXERCISE - EXERCISE (I. MULTI CHOICE QUESTION)
15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES BOOK - NCERT TAMILCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES EXERCISE - EXERCISE (V. NUMERICAL PROBLEMS)
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT TAMILCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - EXERCISE (V. Conceptual Questions)
5 Videos
Similar Questions
A bomb of mass m is thrown with velocity v. It explodes and breaks into two fragments. One fragment of mass m', immediately after the explosion, comes to rest. The speed of the other fragment will be
View SolutionA stone of mass m1 moving at uniform speed v suddenly explodes into two fragments. If the fragment of mass m2 is at rest, the speed of the other fragment is
View Solution
Knowledge Check
A srtone of mass m1 moving at uniform speed v suddenly explodes into two fragments. If the fragment of mass m2 is at rest, the speed of the other fragment is
Am1v(m1−m2)Bm2vm1−m2Cm1v(m1+m2)Dm1vm2A bomb of mass m is thrown with velocity v. It explodes and breaks into two fragments. One fragment of mass m', immediately after the explosion, comes to rest. The speed of the other fragment will be
Amvm−m'Bmvm'CvDmvm+m'A bom of mass 1kg is thrown vertically upwards with a speed of 100m/s. After 5 seconds, it explodes into two fragments. One fragment of mass 400gm is found to go down with a speed of 25m/s. What will happen to the second fragment just after the explosion ? (g=10ms−1)
AIt will go upwards with speed 40m/sBIt will go upwards with speed 100m/sCIt will go upwards with speed 60m/sDIt will go downwards with speed 40m/s
A shell of mass 2m fired with a speed u at an angle θ to the horizontal explodes at the highest point of its trajectory into two fragments of mass m each. If one fragment falls vertically, the distance at which the other fragment falls from the gun is given by :
View SolutionA grenade having mass of 10 kg flying horizontally with a velocity of 10 m/s explodes into two fragments. The larger fragment has a velocity of 25 m/s in the direction of the intial velocity of the grenade. The smaller fragment has a velocity of 12.5 m/s in the opposite dirction. The masses of the fragments are
View SolutionA projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
View SolutionA particle of mass 5 m at rest suddenly breaks on its own into three fragments . Two fragments of mass m of each move along mutully perpendicular direction with speed v each . The energy released suring the process is
View SolutionA grenade having mass of 10 kg flying horizontally with a velocity of 10 m/s explodes into two fragments. The larger fragment has a velocity of 25 m/s in the direction of the intial velocity of the grenade. The smaller fragment has a velocity of 12.5 m/s in the opposite dirction. The masses of the fragments are
View Solution
