Question

Arun and Babu carry a wooden log of mass 28 kg and length 10 m which has almost uniform thickness. They hold it at 1 m and 2 m from the ends respectively. Who will bear more weight of the log? [g = 10 $m{s}^{-2}$]

Explanation

Let us consider the log is in mechanical equilibrium. Hence, the net force and net torque on the log must be zero. The gravitational force acts at the center of mass of the log downwards. It is cancelled by the normal reaction forces `R_(A) and R_(B)` applied upwards by Arun and Babu at points A and B respectively. These reaction forces are the weights borne by them.
The total weight, `W = mg = 28 × 10 = 280 N`, has to be borne by them together. The reaction forces are the weights borne by each of them separately. Let us show all the forces acting on the log by drawing a free body diagram of the log.
For translational equilibrium:
The net force acting on the log must be zero.
`R_(A)+(-mg)+R_(B)=0`
`ul("For rotational equilibrium")`:

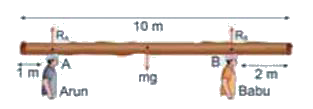
Here, the forces `R_(A) an R_(B)` are taken positive as they act upward. The gravitational force acting downward is taken negative.
`R_(A)+R_(B)=mg`
`ul("For rotational equilibrium")`:

The net torque acting on the log must be zero. For ease of calculation, we can take the torque caused by all the forces about the point A on the log. The forces are perpendicular to the distances. Hence,
`(0R_(A))+(-4mg)+(7R_(B))=0`
Here, the reaction force `R_(A)` cannot produce any torque as the reaction forces pass through the point of reference A. The torque of force mg produces a clockwise turn about the point A which is taken negative and torque of force RB causes anticlockwise turn about A which is taken positive.
`7R_(B)=4mg`
`R_(B)=(4)/(7)mg`
`R_(B)=(4)/(7)xx28xx10=160N`
By substituting for `R_(B)` we get,
`R_(A)=mg-R_(B)`
`R_(A)=28xx10-160=280-160=120N`
As `R_(B)` is greater than `R_(A)`, it is concluded that Babu bears more weight than Arun. The one closer to center of mass of the log bears more weight.