An inductor (L=20mH), a resistor (R=100Ω) and a battery(ɛ=10V) are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value. Solution in Gujrati
(a) The time constant is τ=LR=20mH100Ω=0<br>20ms<br>(b)Themaxiμmcurrentis I = varepsilon /R = (10 V)/(100 Omega) = 0
10 A<br>(c)UsingI = i_0(1-e^(-t/tau), 0
99 i_0 = i_0(1-e^(-t/tau)or, e^(-t/tau) = 0
01)or,(t)/(tau) =- In(0
01)or,t = (0
20ms) In(100) = 0
92ms.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Worked Out Examples29videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer13videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicualr to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
03:02View SolutionA metallic loop is placed in a nonuiform steady magnetic field. Will an emf be induced in the loop?
02:32View SolutionFind the dimensional formula of ε0 .
09:15View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
06:06View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery(ɛ=10V) are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value.
02:28View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (verepsilon = 10 V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the cirucit 1ms after short- circuititig.
01:29View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
03:31View SolutionAn inductor (L=100mH), a resistor (R=100(Ω)) and a battery (E=100V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the point A and B. The current in the circuit 1 ms after the short circuit is
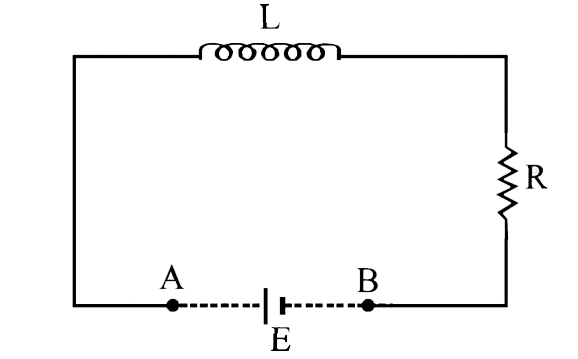 View Solution
View SolutionA 20 mH coil is connected in series with a 2kΩ resistor and a 12 V battery.
Calcualte
(i) time constant of the circuit,
(ii) time during which current decrys to 10% of its maximum value.03:18View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Omega . Calculate the time constant. What will be the maximum value of current in the circuit ?
02:42View SolutionAn inductor (L=100mH), a resistor (R=100Ω), and a battery (W=100V) are initially connected in series as shown by the figure. After a long time the battery is disconnected after short circuiting the points A and B. The currents in the circuit 1mm after the short circuit is
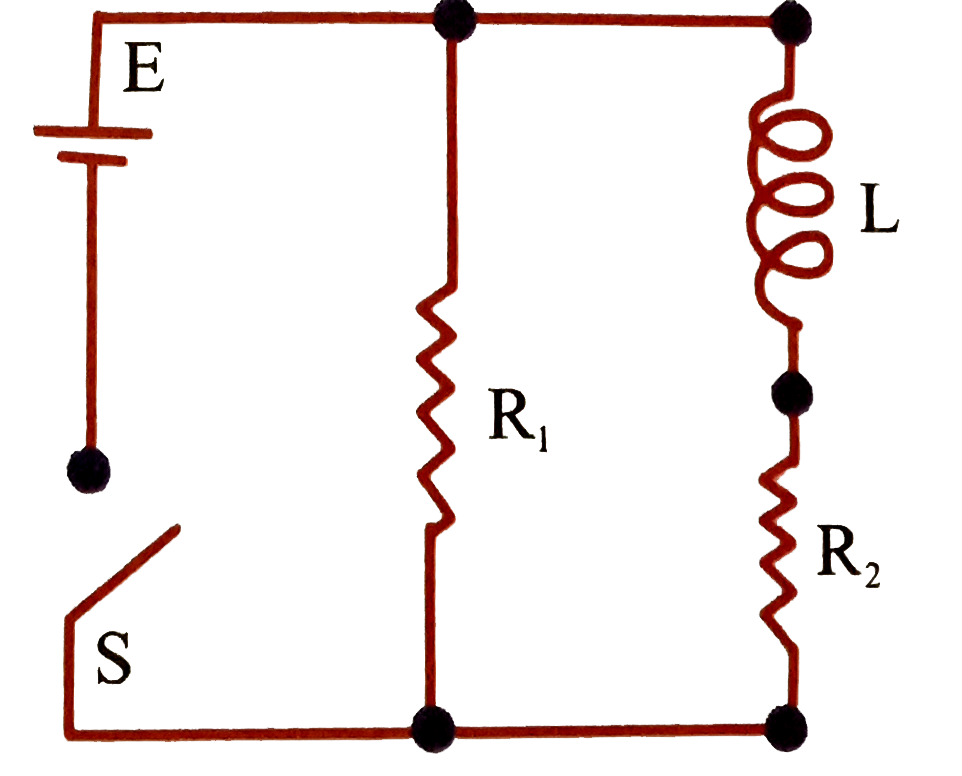 02:55View Solution
02:55View SolutionA 100 V battery, a 5.00 V resistor, and a 10.0 H inductor are connected in series. After the current in th circuit has reached its maximum value.
01:58View SolutionAn L-R combination is connected to an ideal battery. If L=20mH,R=100Ω and ε=10V, find (i) the time constant (ii) the maximum current and (iii) the time elapsed before the current reaches 90% of the maximum value.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery(ɛ=10V) are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (ε=10V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the circuit 1ms after short- circuiting.
03:46View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Omega . Calculate the time constant. What will be the maximum value of current in the circuit ?
02:06View Solution

