According to Van Hiele level of geometric thought the five levels of geometrie understanding are visualisation, analysis, informal deduction, formal deduction and rigour. Students of Class VII are asked to classify the quadrilaterals according to their properties. These students are at ....... level of Van Hiele Geometrical thought.
Visualisation
analysis
informal deduction
formal deduction
The correct Answer is:B
Topper's Solved these Questions
- EVALUATION BOOK - BHARDWAJ ACADEMYCHAPTER - EVALUATION EXERCISE - CHAPTER EXERCISE (Previous Years. Questions)
19 Videos
- ERROR ANALYSISBOOK - BHARDWAJ ACADEMYCHAPTER - ERROR ANALYSISEXERCISE - CHAPTER EXERCISE (Previous Year Questions)
19 Videos
- GEOMETRYBOOK - BHARDWAJ ACADEMYCHAPTER - GEOMETRYEXERCISE - Chapter Exercise (Pervious Years Questions)
25 Videos
Similar Questions
Knowledge Check
According to Van Hiele level of Geometric thought the five levels of geometric understanding are-visualization, Analysis and Informal deduction formal deduction and rigour. Students of class VII are asked to classify the quadrilaterals according to their properties.
These students are at_______ level of Van Hiele Geometrical thought.AVisualizationBAnalysisCInformal DeductionDFormal DeductionAccording to Van Hiele level of Geometric thought, the five levels are visualisation, analysis, informal deduction, formal deduction and rigor. Some polygons are given to a child of Class III for sorting.
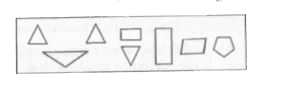
He classified the polygons on the basis of the number of sides. This child is at...... level of Van-Hiele geometrical thoughtAformal deductionBvisualisationCanalysisDinformal deductionAccording to Van Hiele levels of geometry, a student who can sort out rectangles from an assorted collection of shapes are at
ALevel 2: Informal deductionBLevel 3: Formal deductionCLevel 0, VisualisationDLevel 1: Analysis
Children at primary stage are able to classify the given shapes based on their appearance. According to Van Hiele levels to geometry, they are at
View SolutionIn class VI, in the unit of Understanding Quadrilaterals', important results related to angle-sum property of quadrilaterals are introduced using paper folding activity followed by the exercise based on these properties.
At this level proof of the angle property is not given, as the students of class VI are at Van Hiele level of
View SolutionIn Class VI, in the unit of 'Understanding Quadrilaterals", important results related to angle süm property of quadrilaterals are introduced using paper folding activity followed by the exercise based on these properties. At this level, proof of the angle property is not given, as the students of Class VI are at Van Hiele level of
View SolutionIn class VI, in the unit of 'Understanding Quadrilaterals', important results related to angle sum property of quadrilaterals are introduced using paper folding activity followed by the exercise based on these properties. At this level, proof of the angle property is not given as the students of Class VI are at Van Hiele level of
View SolutionStudents are asked to establish a relation between vertically opposite angles. They draw various figures, measure the angles and observe that vertically opposite angles are equal. In this case, students according to Van Hiele thought are at
View Solution
