Calculate total number of peaks which may appear in the radial probability curves for the following state in H atom?
$Ψ n, 1 = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{1}{90})}^{3 / 2} (6 - \frac{4 r}{a_{0}} + \frac{4}{9} \frac{r^{2}}{a_{0}^{2}}) e_{0}^{- r / 3 a_{0}}$

Text Solution

Verified by Experts

The correct Answer is:3

3

Class 12 CHEMISTRY QUESTION BANK

Topper's Solved these Questions

NTA TPC JEE MAIN TEST 57BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 57EXERCISE - CHEMISTRY
30 Videos
NTA TPC JEE MAIN TEST 59BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 59EXERCISE - CHEMISTRY
30 Videos

Knowledge Check

Given $R (r) = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{1}{a_{0}})}^{3 / 2} (6 - \frac{4 r}{a_{0}} + \frac{4}{9} \frac{r^{2}}{a_{0}^{2}}) e .^{\frac{r}{3 a_{0}}}$
Which in INCORRECT statement about R(r ).
AThe number of angular nodes is zero.
BThe number of radii nodes is 2.
CThe distance between radial nodes is $\sqrt{27} a_{0}$ .
DThe equation represents 2s orbital
The Schrodinger wave equation for H-atom is
$\nabla^{2} Ψ = \frac{8 π^{2} m}{h^{2}} (E - V) Ψ = 0$
Where $\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}}$
E = Total energy and V=potential energy wave function $Ψ_{(\begin{matrix} r & θ & ϕ \end{matrix})} R_{(r)} Θ_{(θ)} Φ_{(ϕ)}$
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. $Θ$ and $Φ$ are angular wave function. $R^{2}$ is known as radial probability density and $4 π r^{2} R^{2} d r$ is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
$Ψ_{1 s} = \sqrt{\frac{1}{π a_{0}^{a}}} e_{r}^{- z_{r} / a_{0}}$
$Ψ_{2 s} = {(\frac{Z}{2 a_{0}})}^{½} (1 - \frac{Z r}{a_{0}}) e^{- \frac{Z r}{a_{0}}}$
The plot of radial probability function $4 π r^{2} R^{2}$ aganist r will be:

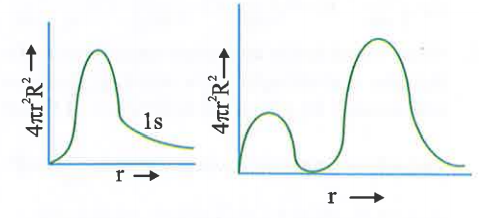
Answer the following questions:
The following graph is plotted for ns-orbitals

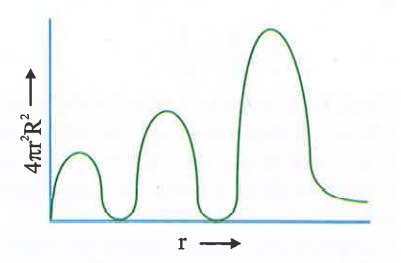
The value of 'n' will be:
A1
B2
C3
D4
The wave function of 3s and $3 p_{z}$ orbitals are given by :
$Ψ_{3 s} = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{Z}{σ_{0}})}^{3 / 2} (6 = 6 σ + σ) e^{- σ / 2}$
$Ψ_{3 s_{z}} = \frac{1}{9 \sqrt{6}} {(\frac{3}{4 π})}^{1 / 2} {(\frac{Z}{σ_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2} cos 0,$
$σ = \frac{2 Z r}{n α_{0}}$
where $α_{0} = 1 s t$ Bohr radius , Z= charge number of nucleus, r= distance from nucleus.
From this we can conclude:
ATotal number of nodal surface is same for 3s and $3 p_{x}$ orbitals
BThe angular nodal surface of $3 p_{z}$ orbital occur at $0 = \frac{π}{2}$
CThe radial nodal surface of 3s and $3 p_{z}$ orbitals are at equal distance from nucleus.
D3s electrons have greater penetrating power into the nucleus compared to $3 p_{z}$ electron.

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 58-CHEMISTRY

Home
Ask Doubt
Profile

Calculate total number of peaks which may appear in the radial probability curves for the following state in H atom? Ψn,1=19√3(14π)1/2(190)3/2(6−4ra0+49r2a20)e−r/3a0

The correct Answer is:3

3

Topper's Solved these Questions

Similar Questions

Knowledge Check

Given R(r)=19√3(14π)1/2(1a0)3/2(6−4ra0+49r2a20)e.r3a0 Which in INCORRECT statement about R(r ).

The wave function of 3s and 3pz orbitals are given by : Ψ3s=19√3(14π)1/2(Zσ0)3/2(6=6σ+σ)e−σ/2 Ψ3sz=19√6(34π)1/2(Zσ0)3/2(4−σ)σe−σ/2cos0, σ=2Zrnα0 whereα0=1st Bohr radius , Z= charge number of nucleus, r= distance from nucleus. From this we can conclude:

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 58-CHEMISTRY

Calculate total number of peaks which may appear in the radial probability curves for the following state in H atom?
$Ψ n, 1 = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{1}{90})}^{3 / 2} (6 - \frac{4 r}{a_{0}} + \frac{4}{9} \frac{r^{2}}{a_{0}^{2}}) e_{0}^{- r / 3 a_{0}}$

Given $R (r) = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{1}{a_{0}})}^{3 / 2} (6 - \frac{4 r}{a_{0}} + \frac{4}{9} \frac{r^{2}}{a_{0}^{2}}) e .^{\frac{r}{3 a_{0}}}$
Which in INCORRECT statement about R(r ).