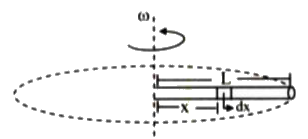
A uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
The correct Answer is:03.00
Y=FLAl
Here, F =centrifugal force due to rotation.
∴L=FLAY
From the figure, considering small elongation dx of length segment x dl=dF×xAY….(i)
where, dF =centrifugal force of differential mass dM
but dF=dMω2x=(ρAdx)ω2x
=ρAω2xdx
Substuiting in equation (i),
∴dl=(ρAω2xdx)×xAY
Intergrating over limits,
∴∫l0dl=ρω2Y∫L0=ρω2)3Y[L3−0)
∴l=ρω2L33Y
⇒n=3
Topper's Solved these Questions
Similar Questions
A uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
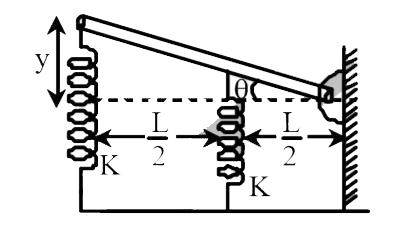
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation - Question 2 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 3 - Select One

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθ
A thin uniform metallic rod of length 0.5 m and radius 0.1 m rotates with an angular velocity 400rad/s is a horizontal plane about a vertical axis passing through one of its ends. Calculate (a) tenstion in the rod and (b) the elogation of te rod. The density of material of the rod is 104kg/m3 and the young's modulus is 2×1011N/m2
View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View SolutionA long uniform rod of length L and mass M is free to rotate in a horizontal plane about a vertical axis through its one end 'O'. A spring of force constant k is connected between one end of the rod and PQ. When the rod is in equilibrium it is parallel to PQ.

(a)What is the period of small oscillation that result when the rod is rotated slightly and released ?
(b) What will be the maximum speed of the displacement end of the rod, if the amplitude of motion is θ0?View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
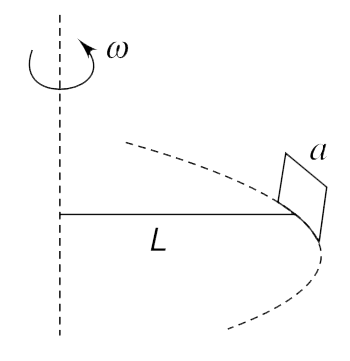
View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
 View Solution
View Solution

