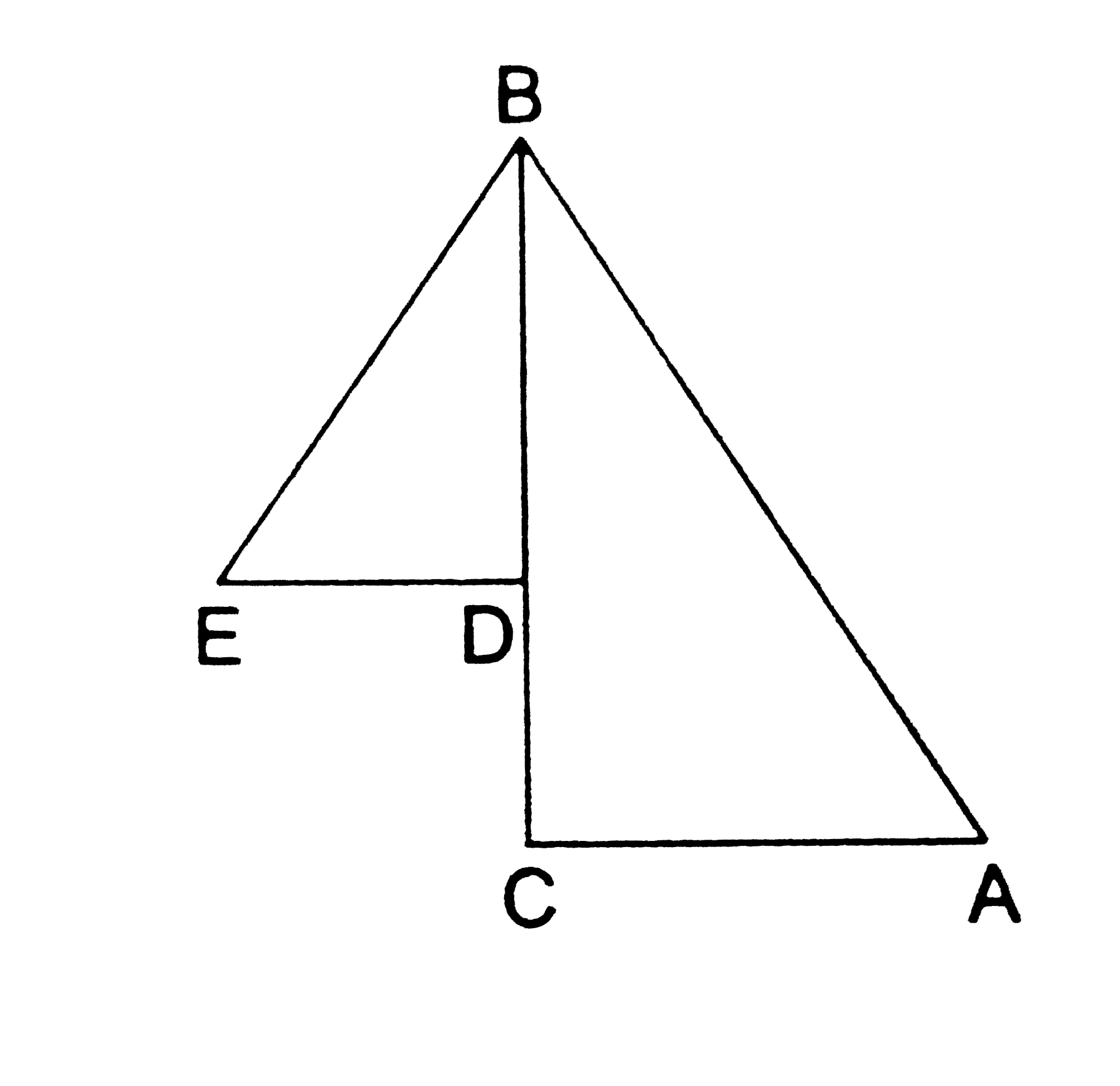
In figure, line segment DF intersects the side AC of a ΔABC at the point E such that E is the mid-point of CA and ∠AEF−∠AFE. Prove that BDCD=BFCE

Step by step video & image solution for In figure, line segment DF intersects the side AC of a DeltaABC at the point E such that E is the mid-point of CA and angleAEF-angleAFE. Prove that (BD)/(CD)=(BF)/(CE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - BOARD CORNER ( VERY SHORT ANSWER TYPE QUESTION ( 1 MARK EACH ))
4 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - BOARD CORNER ( SHORT ANSWER TYPE QUESTION ( 3 MARK EACH ))
6 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT EXEMPLAR ( EXERCISE - 6.3 )
15 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
Knowledge Check
In the given figure, M is the mid-point of both AC and BD. Then
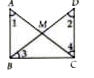 A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3
A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3
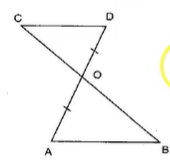
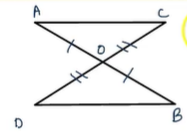
In Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
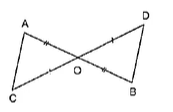
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIn Figure O is the mid-point of aB and CD. Prove tat AC=BD and AC||BD.

View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
View SolutionIn Figure, O is the mid point of AB and CD . Prove that AOC≅BOD AC=BD (iii) ACBD
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE.Show that ΔABD≅ΔACE.
View Solution