Question

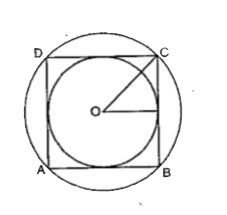
The side of a square is 10 cm. Find the area between inscribed and circumscribed circles of the square.

Explanation

To find the area between the inscribed and circumscribed circles of a square with a side length of 10 cm, we will follow these steps:

Step 1: Calculate the radius of the inscribed circle
The inscribed circle (also known as the incircle) is the circle that fits perfectly inside the square. The radius \( r \) of the inscribed circle is half the length of the side of the square.

\( r = \frac{\text{side}}{2} = \frac{10 \, \text{cm}}{2} = 5 \, \text{cm} \)

Step 2: Calculate the area of the inscribed circle
The area \( A \) of a circle is given by the formula:

\( A = \pi r^2 \)

Substituting the radius we found:

\( A_{\text{inscribed}} = \pi (5 \, \text{cm})^2 = \pi \times 25 \, \text{cm}^2 \)

Using \( \pi \approx \frac{22}{7} \):

\( A_{\text{inscribed}} = \frac{22}{7} \times 25 = \frac{550}{7} \, \text{cm}^2 \)

Step 3: Calculate the radius of the circumscribed circle
The circumscribed circle (also known as the circumcircle) is the circle that passes through all the vertices of the square. The radius \( R \) of the circumscribed circle is half the length of the diagonal of the square.

First, we calculate the diagonal \( d \) of the square using the formula:

\( d = \sqrt{2} \times \text{side} = \sqrt{2} \times 10 \, \text{cm} = 10\sqrt{2} \, \text{cm} \)

Now, the radius \( R \) is:

\( R = \frac{d}{2} = \frac{10\sqrt{2} \, \text{cm}}{2} = 5\sqrt{2} \, \text{cm} \)

Step 4: Calculate the area of the circumscribed circle
Using the area formula for a circle:

\( A_{\text{circumscribed}} = \pi R^2 \)

Substituting the radius we found:

\( A_{\text{circumscribed}} = \pi (5\sqrt{2} \, \text{cm})^2 = \pi \times 25 \times 2 = 50\pi \, \text{cm}^2 \)

Using \( \pi \approx \frac{22}{7} \):

\( A_{\text{circumscribed}} = 50 \times \frac{22}{7} = \frac{1100}{7} \, \text{cm}^2 \)

Step 5: Find the area between the inscribed and circumscribed circles
To find the area between the two circles, we subtract the area of the inscribed circle from the area of the circumscribed circle:

\( \text{Area between} = A_{\text{circumscribed}} - A_{\text{inscribed}} \)

\( = \frac{1100}{7} \, \text{cm}^2 - \frac{550}{7} \, \text{cm}^2 = \frac{1100 - 550}{7} \, \text{cm}^2 = \frac{550}{7} \, \text{cm}^2 \)

Final Answer
The area between the inscribed and circumscribed circles of the square is:

\( \frac{550}{7} \, \text{cm}^2 \approx 78.57 \, \text{cm}^2 \)