A chord of a circle of radius 12 cm subtends an angle of 60° at the centre. Find the area of the corresponding segment of the circle.
( Use π=3.14,√3=1.73 )
The correct Answer is:13.08 cm2
To find the area of the segment of a circle defined by a chord that subtends an angle of 60° at the center of a circle with a radius of 12 cm, we can follow these steps:
1. Identify the Given Values:
- Radius of the circle (r) = 12 cm
- Central angle (θ) = 60°
2. Calculate the Area of the Sector:
The formula for the area of a sector is given by:
Area of Sector=πr2θ360
Substituting the values:
Area of Sector=3.14×(12)2×60360
=3.14×144×60360
=3.14×8640360
=27178.4360=75.49 cm2
3. Calculate the Area of Triangle OAC:
Since triangle OAC is an isosceles triangle with two sides equal to the radius (12 cm) and the angle at the center being 60°, it is also an equilateral triangle.
The area of an equilateral triangle can be calculated using the formula:
Area=√34a2
where a is the length of a side. Here, a=12 cm.
Area of Triangle OAC=√34×(12)2
=√34×144=36√3
Using √3=1.73:
=36×1.73=62.28 cm2
4. Calculate the Area of the Segment:
The area of the segment is given by:
Area of Segment=Area of Sector−Area of Triangle OAC
Substituting the values calculated:
Area of Segment=75.49−62.28=13.21 cm2
Final Answer:
The area of the corresponding segment of the circle is approximately 13.21 cm².
- Radius of the circle (r) = 12 cm
- Central angle (θ) = 60°
The formula for the area of a sector is given by:
Area of Sector=πr2θ360
Substituting the values:
Area of Sector=3.14×(12)2×60360
=3.14×144×60360
=3.14×8640360
=27178.4360=75.49 cm2
Since triangle OAC is an isosceles triangle with two sides equal to the radius (12 cm) and the angle at the center being 60°, it is also an equilateral triangle.
The area of an equilateral triangle can be calculated using the formula:
Area=√34a2
where a is the length of a side. Here, a=12 cm.
Area of Triangle OAC=√34×(12)2
=√34×144=36√3
Using √3=1.73:
=36×1.73=62.28 cm2
The area of the segment is given by:
Area of Segment=Area of Sector−Area of Triangle OAC
Substituting the values calculated:
Area of Segment=75.49−62.28=13.21 cm2
The area of the corresponding segment of the circle is approximately 13.21 cm².
Similar Questions
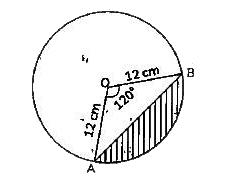
A chord of a circle of radius 12 cm subtends an angle of 120∘ at the centre . Find the area of the corresponding segment of the circle.
View SolutionA chord of a circle of radius 12 cm subtends an angle of 120∘ at the centre.
Find the area of the corresponding segment of the circle (Use π=3.14 and √3=1.73)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A chord of a circle of radius 28 cm makes an angle of 90∘ at the centre. Find the area of the major segment.
A1456 cm2B1848 cm2C392 cm2D2240 cm2
A chord of a circle of radius 12 cm subtands an angle of 120∘ at the centre. Find the aera of the corresponding segment of the circle. (Useπ=3.14,√3=1.73)
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding sector.
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Minor segmentView SolutionA chord of a circle of radius 15 cm subtends an angle of 60∘ at the centre . Find the areas of the corresponding minor and major segments of the circle.
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Major sectorView SolutionA chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of the sector.
View SolutionIn a circle of radius 21 cm and arc subtends an angle of 60∘ at the centre. Find the area of the sector.
View Solution

