Find the area of the shaded region in figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-point P, Q, R and S of the sides AB, BC, CD and DA, respectively of a square ABCD. (Use π=3.14 )
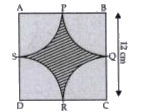
The correct Answer is:30.85 cm2
Step by step video, text & image solution for Find the area of the shaded region in figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-point P, Q, R and S of the sides AB, BC, CD and DA, respectively of a square ABCD. (Use pi = 3.14 ) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Find the area of the shaded region in figure, in figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-point P, Q, R and S of the sides AB, BC, CD and DA, respectively of a square ABCD. (use π=3.14)

View SolutionFind the area of the shaded region in Fig. 3, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA respectively of a square ABCD of side 12 cm. [Use π=3.14]
View SolutionFind the area of the shaded region in figure where ABCD is a square of side 14 cm.

View SolutionFind the area of the shaded region in Fig where ABCD is a square of side 14 cm.
View SolutionFind the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionFind the area of the shaded region in Fig. 15.48, where ABCD is a square of side 10 cm. (Use π=3.14) (FIGURE)
View Solution