In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O' are centres of the circles. Find the area of shaded region
The correct Answer is:1708 cm2
Step by step video & text solution for In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O' are centres of the circles. Find the area of shaded region by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O' are centres of the circles. Find the area of shaded region
View SolutionIn the given figure ABCD is a square of side 4cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region.
[Use π=3.14]

View Solution
Knowledge Check
The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
A2π:1B1:√πC√π:1D1:πThe areas of a square and a circle are equal. The radius of the circle is r and the side of the square is S.Find the circumference of the circle in terms of S.
ASB2SC3SD4SThe radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
A1:πBπ:1Cπ:2D2:π
in the adjoining figure ABCD is a square of side 14 cm. Find the radius of the circle
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

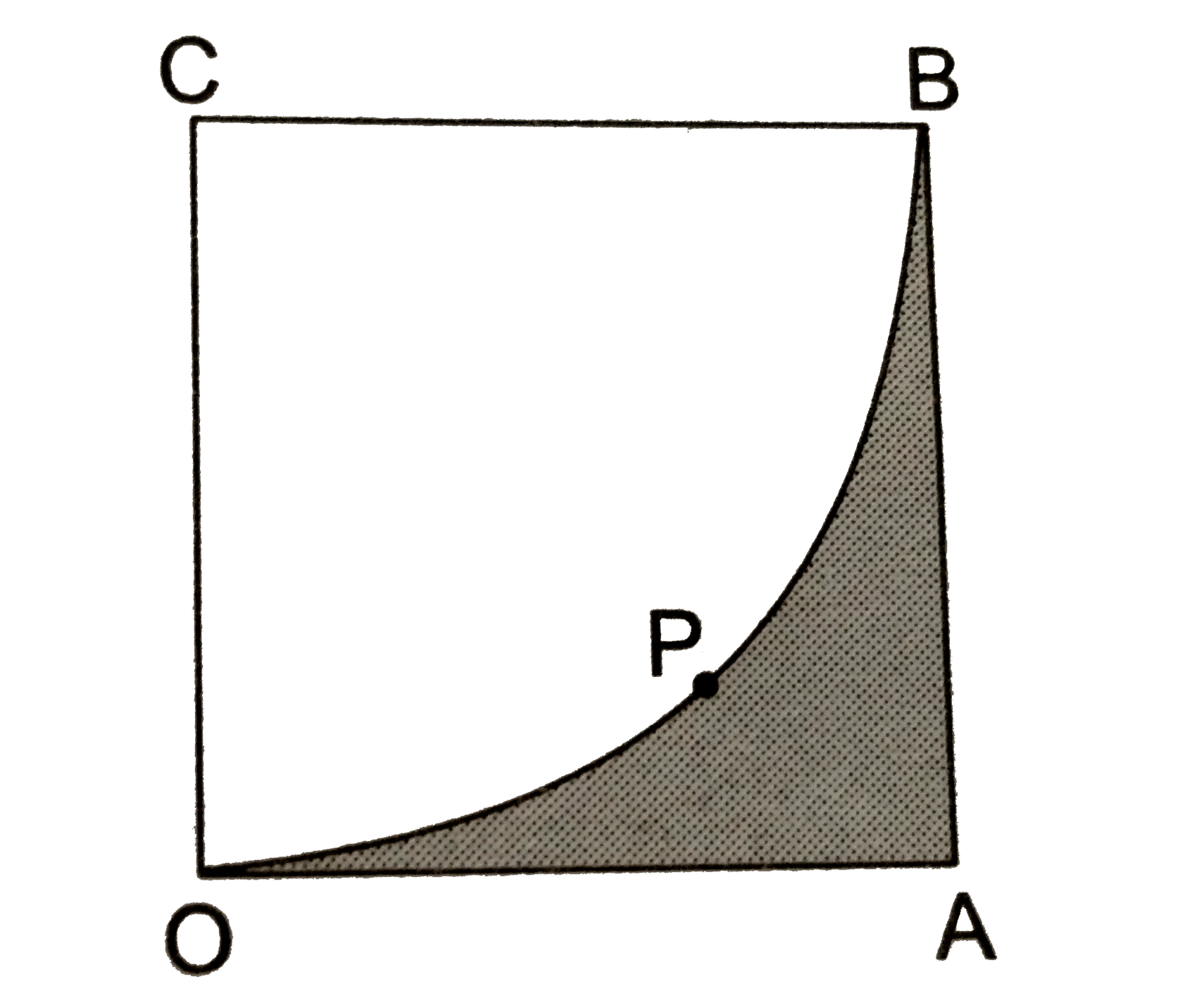
View SolutionIn the given figure, OABC is a square of side 7cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
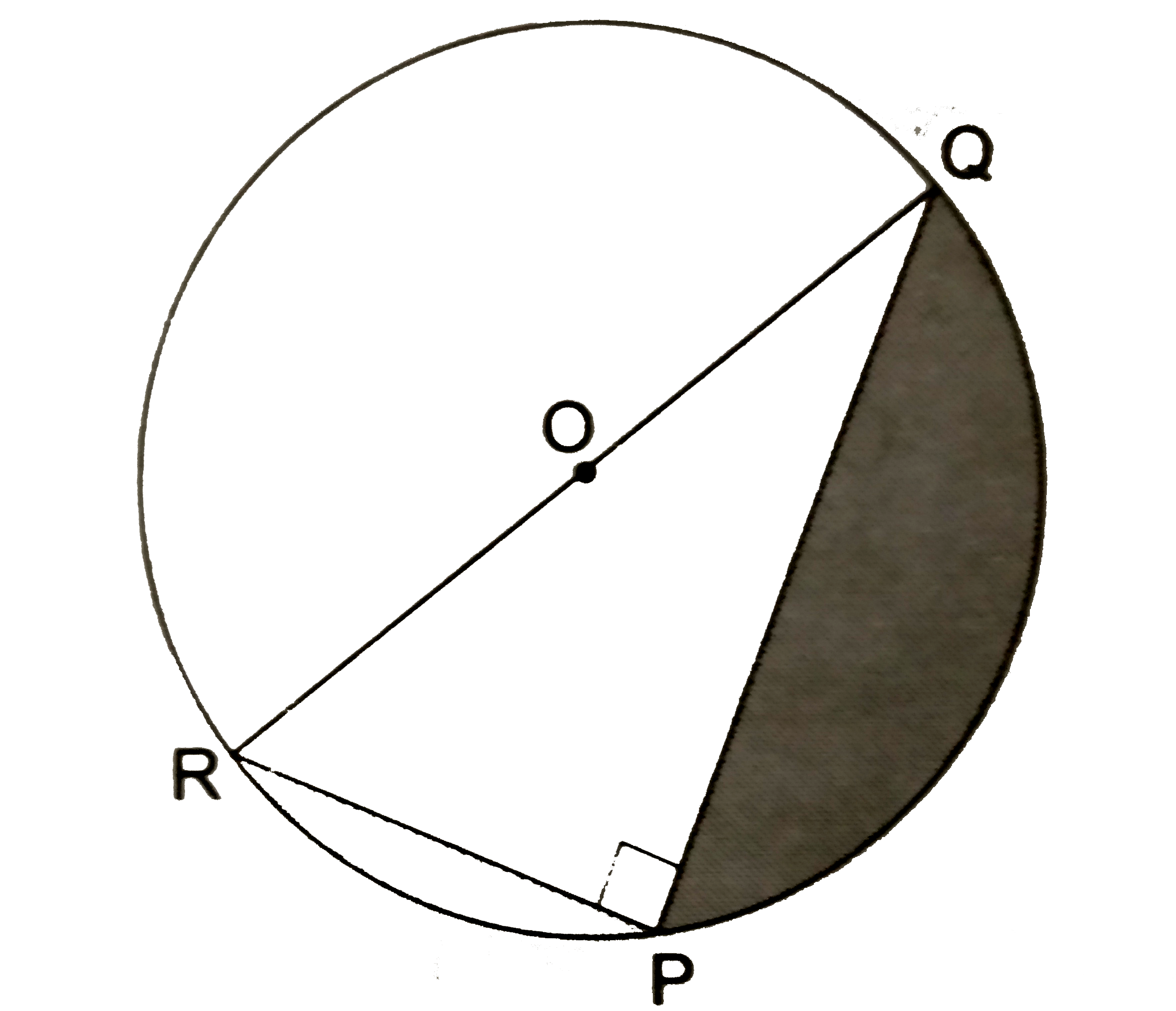
View SolutionIn the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
View Solution
