θ=30∘ लेकर निम्नलिखित में प्रत्येक को सत्यापित कीजिये-
cos2θ=2cos2θ−1=1−2sin2θ
Step by step video & image solution for theta= 30^(@) लेकर निम्नलिखित में प्रत्येक को सत्यापित कीजिये- cos 2 theta= 2 cos^(2) theta- 1= 1 -2 sin^(2) theta by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 11B (बहुवैकल्पिक प्रश्न)
23 Videos
- कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 11B (बहुवैकल्पिक प्रश्न)
23 Videos
- ऊँचाई तथा दूरी BOOK - BHARATI BHAWANCHAPTER - ऊँचाई तथा दूरी EXERCISE - प्रश्नमाला 14B (बहुवैकल्पिक प्रश्न)
10 Videos
- त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 10B (बहुवैकल्पिक प्रश्न)
13 Videos
Similar Questions
(sec260∘−1)=?
View Solution(sec260∘−1)=?
View Solutionदी गई आकृति में बिंदु C का बिंदु A से देखना दर्शाया गया है। A से अवनमन कोण है
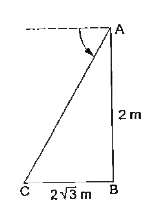
View Solutionयदि tanθ=815 हो, तो cosecθ=?
View SolutionIf sin(theta)_(1)+sin(theta)_(2)+sin(theta)_(3)=1 then cos(theta)_(1)+cos(theta)_(2)+cos(theta)_(3)=
View SolutionProve the following identity: (1sec2θ−cos2θ+1cosec2θ−sin2θ)sin2θcos2θ=1−sin2θcos2θ2+sin2θcos2θ
View Solution(cos^(2)theta(1-cos theta))/(sin^(2)theta(1-sin theta))=(1+sin theta)/(1+cos theta)
View Solutionयदि θ=30∘, तब सिद्ध कीजिए कि
cos2θ=2cos2θ−1=1−2sin2θ=cos2θ−sin2θ
View Solution(1sec2−cos2θ+1cosec2θ−sin2θ)sin2θcos2θ=1−sin2θcos2θ2+sin2θcos2θ
View Solutionसिद्ध कीजिए : (1sec2θ−cos2θ+1 cosec 2θ−sin2θ).sin2θcos2θ=1−sin2θcos2θ2+sin2θcos2θ
View Solutionसिद्ध करें कि
11−cosθ−11+cosθ=2cosθsin2θ=2cotθ⋅cosecθ.
View Solutionsin2θ1−cosθ−cos2θ1−sinθ=cosθ−sinθ
View SolutionIf ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0, then the value of θ is
View SolutionProve that, 1+sin2θ−cos2θsinθ+cosθ=2sinθ
View SolutionIf cosθ+cos2θ=1 then sin2θ+2sin2θ+sin2θ=
View SolutionIf ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0, then the value of θ is
View Solution
