यदि A और B दो न्यूनकोण ऐसे हो कि tanA=13,tanB=12 तथा tan(A+B)=tanA+tanB1−tanAtanB, तो सिद्व कीजिये कि A+B=45∘
Step by step video & image solution for यदि A और B दो न्यूनकोण ऐसे हो कि tan A= (1)/(3), tan B= (1)/(2) तथा tan (A+B) = (tan A + tan B)/(1- tan A tan B), तो सिद्व कीजिये कि A +B= 45^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 11B (बहुवैकल्पिक प्रश्न)
23 Videos
- कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 11B (बहुवैकल्पिक प्रश्न)
23 Videos
- ऊँचाई तथा दूरी BOOK - BHARATI BHAWANCHAPTER - ऊँचाई तथा दूरी EXERCISE - प्रश्नमाला 14B (बहुवैकल्पिक प्रश्न)
10 Videos
- त्रिकोणमितीय अनुपात BOOK - BHARATI BHAWANCHAPTER - त्रिकोणमितीय अनुपात EXERCISE - प्रश्नमाला 10B (बहुवैकल्पिक प्रश्न)
13 Videos
Similar Questions
(sec260∘−1)=?
View Solution(sec260∘−1)=?
View Solutionदी गई आकृति में बिंदु C का बिंदु A से देखना दर्शाया गया है। A से अवनमन कोण है
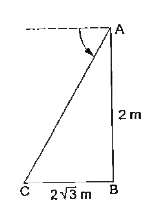
View Solutionयदि tanθ=815 हो, तो cosecθ=?
View SolutionIf tan A=(1)/(2) and tan B=(1)/(3), then tan(2A+B) is
View SolutionFor all values of A and B tan(A+B)=tanA+tanB1−tanAtanB and tan(A−B)=tanA−tanB1+tanAtanB
View SolutionProve that tan(A+B+C)=tanA+tanB+tanC−tanAtanBtanC1−tanAtanB−tanBtanC−tanCtanA
View SolutionIf A and B are acute angles such that tanA=12 , tanB=13 and tan(A+B)=tanA+tan B1−tanAtanB , find A+B .
View SolutionProve that: tan(A+B)cot(A−B)= tan2A−tan2B1−tan2Atan2B
View SolutionIf A+B=45∘, then (1+tanA)(1+tanB)=__________
View Solutionनिम्नलिखित का मान बताइये :
tanA+tanB1−tanA⋅tanB,यदि A=1√2 और cosB=√32
View Solutionयदि A तथा B न्यूनकोण इस प्रकार है कि tanA=12,tanB=13 तथा tan(A+B)=tanA+tanB1−tanAtanB, तो A+B का मान ज्ञात करो ।
View SolutionIf tanA=12 and tanB=13, then tan(A+B) is equal to
View Solutiontan(A+B)=tanA+tanB1−tanAtanB
View SolutionIf A+B=π2⇒TanATanB=1,⇒Tan(A−B)=tanA−tanB1+tanAtanB=tanA−tanB2,⇒tanA=tanB+2tan(A−B),
x=Tan5π28+2Tanπ7 Then x
View SolutionProve that tan(A−B)=tanA−tanB1+tanA⋅tanB , if A=60° & B=45°.
View Solution
