If the given triangles ΔABCandΔEFG are congruent, determine whether the given pair of sides and angles are corresponding sides or corresponding angles or not .
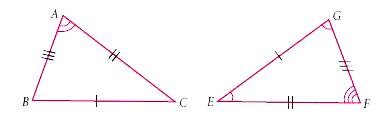
∠Aand∠G
The correct Answer is:Not corresponding angles
Similar Questions
Identify each of the given pair of angles as alternate angles, co-interior angles or corresponding angles or none of these in the given figure:

∠4,∠8
View SolutionIdentify each of the given pair of angles as alternate angles, co-interior angles or corresponding angles or none of these in the given figure:

∠1,∠6
View Solution
Knowledge Check
If the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
A2:3:1B√3:2:1C2:√3:1D1:√3:2If the angles of a triangle are in the ratio 1:2:3,the corresponding sides are in the ratio
A2:3:1B√3:2:1C2:√3:1D1:√3:2Assertion : In a quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure) then ΔACB≅ΔADB by SAS congruence criteria.
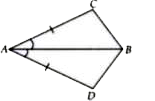
Reason : Two triangles are congruent if two sides and the included angle of one triangle is equal to the corresponding two sides and included angle of the other.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
Identify each of the given pair of angles as alternate angles, co-interior angles or corresponding angles or none of these in the given figure:

∠5,∠2
View SolutionWhich of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.
View SolutionIf △ABC△PQR, then write the corresponding angles of the two triangles and write the ratios of corresponding sides.
View SolutionIf two triangles are similar; prove that the ratio of the corresponding sides is same as the corresponding angle bisector segments.
View SolutionConsider the following statements : Two triangles are said to be congruent, if
1. Three angles of one triangle are equal to the corresponding three angles of the other triangle.
2. Three sides of one triangle are equal to the corresponding three sides of the other triangle,
3. Two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
4. Two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
Which of the above statements are correct ?
View Solution
