A container is filled with water (μ = 4/3) upto a height of 36 cm. Now a concave mirror is placed 12 cm above the water level and it was seen that the image of an object placed at the bottom of container is formed 10 cm below the water level. The focal length of the mirror is ___ cm.
The correct Answer is:13
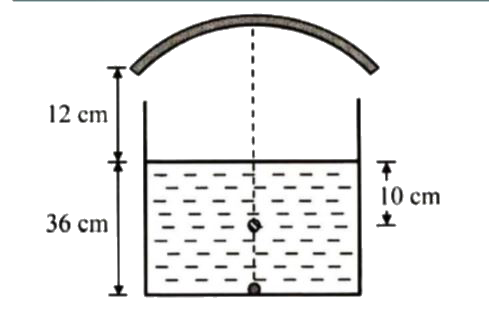
As object is placed in water, the object distance from mirror will be apparent.
∴ Apparent distance
= Real distanceμ=(364/3)=27cm
Distance of object from mirror Distance of mirror Apparent distance = from water level + of object
= 12 + 27 = 39cm
Similarly, distance of image from mirror
=12+⎛⎝1043⎞⎠=12+7.5=19.5cm
For mirror,
1v+1u=1f
Considering sign conventions for mirror,
∴1−19.5−139=1f
∴1f=−2−139=−339
∴ f = - 13cm
Neglecting negative sign, focal length = 13cm
Topper's Solved these Questions
Similar Questions
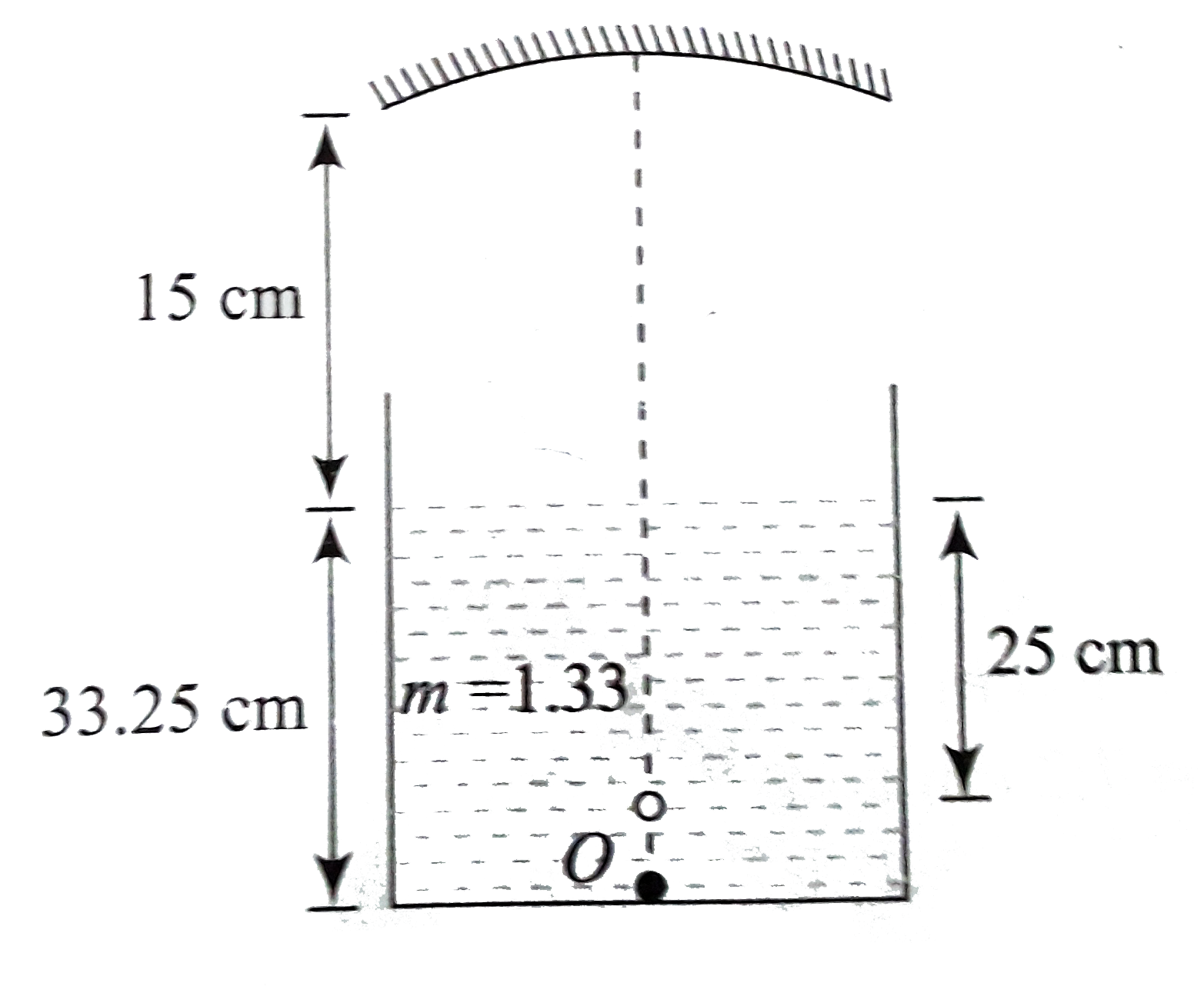
A container is filled with water (μ=1.33) upto a height of 33.25cm. A convex mirror I s placed 15cm above the water level and image of an object placed at the bottom is formed 25cm below the water level. Focal length of the mirror is
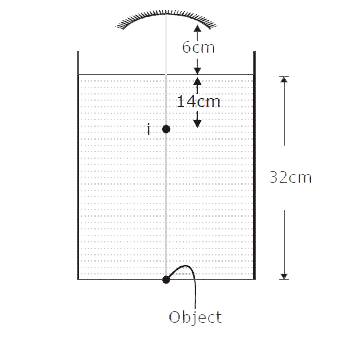
View SolutionA beaker contains water (μ=4/3) filled to a height of 32 cm. A concave mirror is fixed 6 cm above the surface of water as shown in figure. An object is placed at the bottom of the beaker and its image is formed 14 cm below the surface of water. The focal length of the mirror is
View Solution
Knowledge Check
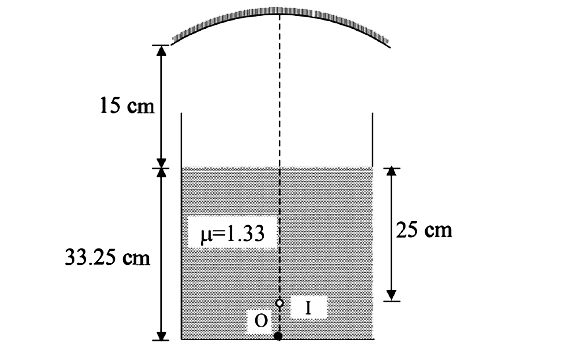
A container is filled with water (μ=1.33) upto a height of 33.25 cm. A concave mirror is placed 15cm above the water level and the image of an object placed at the bottom is formed 25 cm below the water level. Focal length of the mirror is
 A15 cmB20 cmC−18.31cmD10 cm
A15 cmB20 cmC−18.31cmD10 cmA container is filled with water (μ=1.33) upto a height of 33.25cm. A convex mirror I s placed 15cm above the water level and image of an object placed at the bottom is formed 25cm below the water level. Focal length of the mirror is
 A15cmB20cmC−18.31cmD10cm
A15cmB20cmC−18.31cmD10cmA container is filled with water (μ=1.33) up to height of 33.2cm. A concave mirror is placed 15 cm above the water level. Image of an object placed at the bottom is formed at the same place. The focal length of mirror is :
 A10 cmB15 cmC-20 cmD2 cm
A10 cmB15 cmC-20 cmD2 cm
Find the position of the image of an object placed at a distance of 12 cm from a convex mirror of focal length 10 cm.
View SolutionFor an object placed at a distance 20 cm from a concave mirror, the image is formed at the same position. What is the focal length of the mirror?
View SolutionAn object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
View SolutionThe focal length of a concave mirror is 12 cm . Where should an object of length 4 cm be placed so that a real image of 1 cm length is formed ?
View SolutionAn object is placed 10 cm in front of a convex mirror of focal length 20 cm . The distance of the image from the mirror is
View Solution
