Two particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
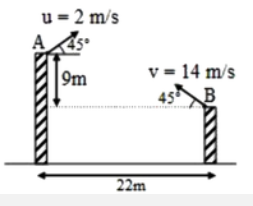
The correct Answer is:6
vx=8√2s−1= relative velocity
along x-axis
∴x=(22−8√2t)
vy=6√2m/s= relative velcoity along the y-axis
∴y=(9−6√2t)
r=√x2+y2
For minimum r,
drdt=0⇒t=2310√2s
r=√x2+y2
Substitutingk the value of t in r,
rmin=6m
Topper's Solved these Questions
Similar Questions
Two particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.View Solution
Knowledge Check
- Question 1 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
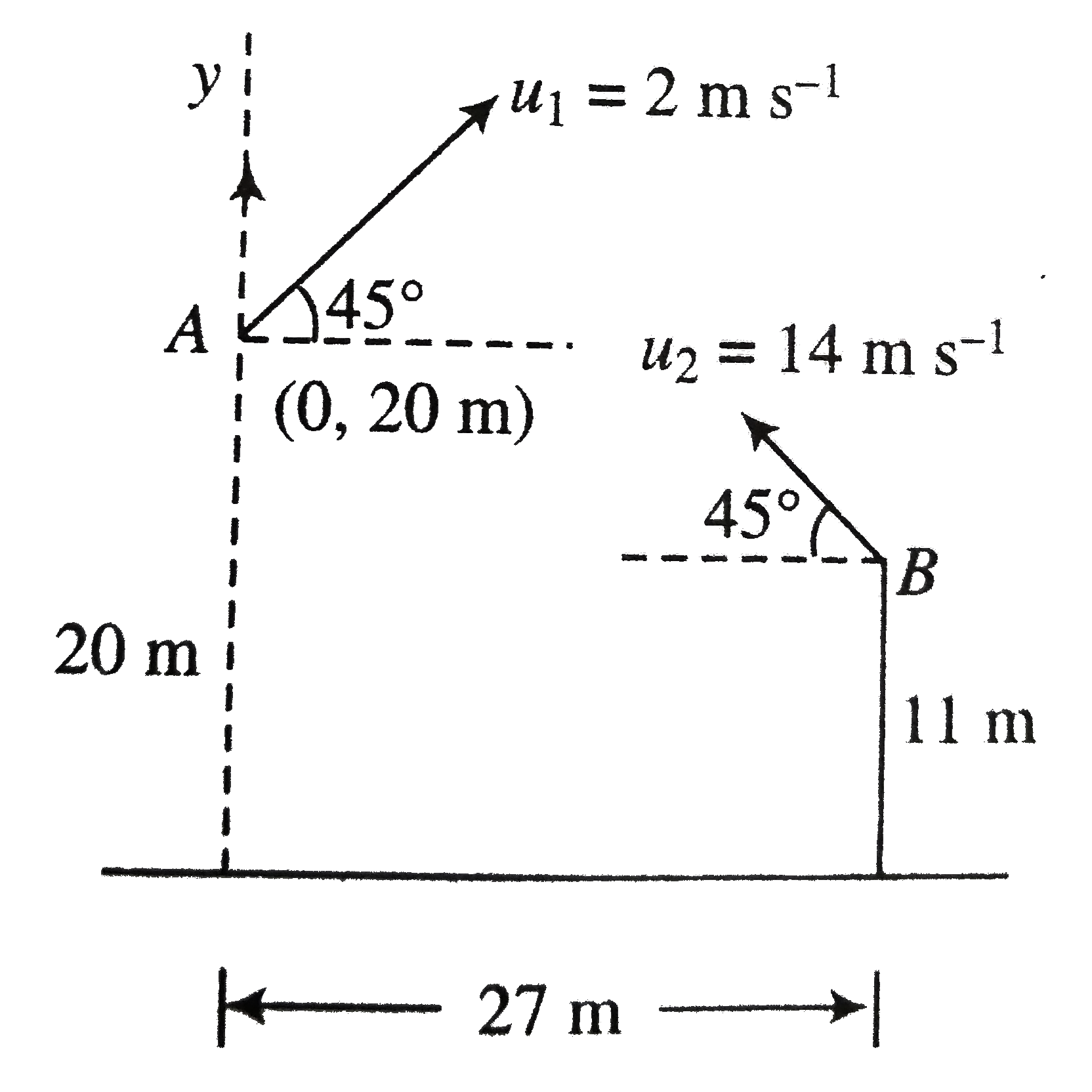
Minimum separation between A and B isA3 mB6 mC12 mD9 m - Question 2 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
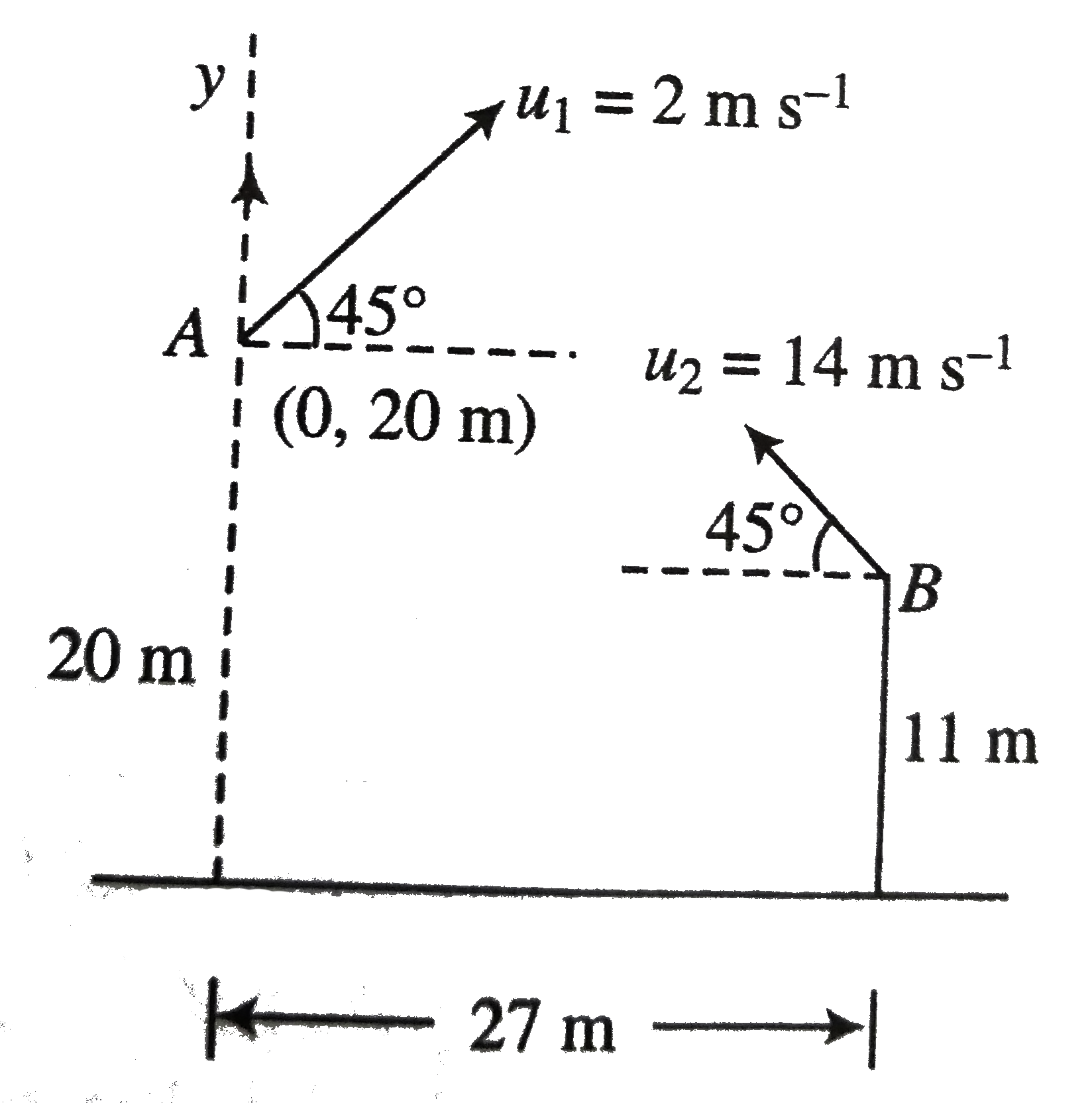
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆj - Question 3 - Select One
Two particles move in a uniform gravitational field with an acceleration g.At the initial moment the particles were located at same point and moved with velocities u1=9ms−1 and u2=4ms−1 horizontally in opposite directions.The time between the particles at the moment when their velocity vectors are mutually perpendicular in s in (take g=10ms−2)
A0.36B3.6C0.6D6
Two particles A and B are thown vertically upward with velocity, vertically upward with velocity, 5ms−1 and 10ms−1 respectively (g=10 m s^(-2)), Find separation between them after 1s.
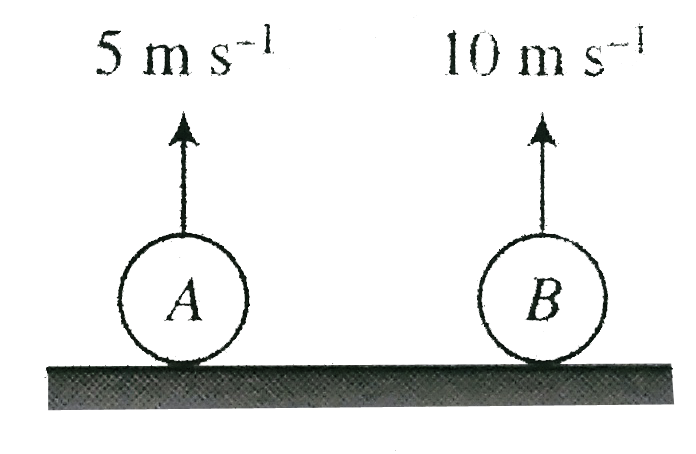 .View Solution
.View SolutionFive particles are projected simultaneously from the top of a tower that is h=32m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal.
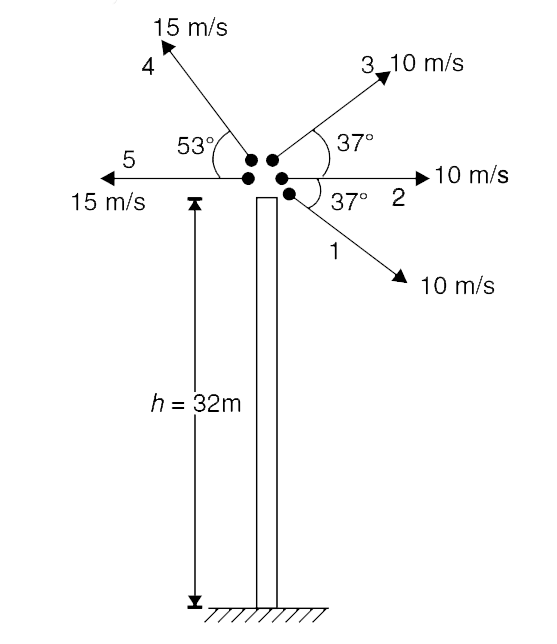
(a) Which particle will hit the ground first?
(b) Separation between which two particles is maximum at the instant the first particle hits the ground?
(c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground.
[g=10m/s2,tan37∘=34]View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
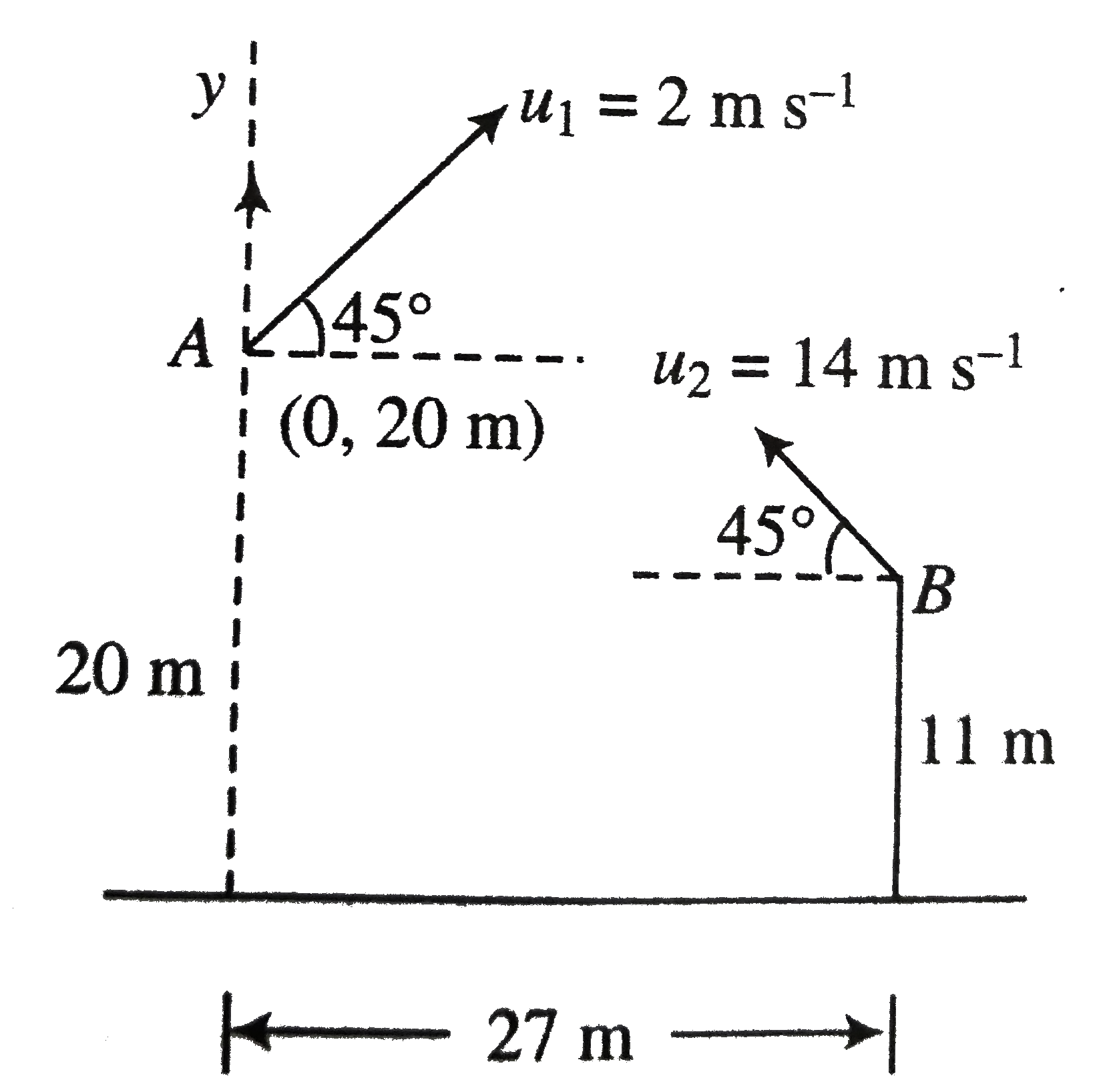
The direction (angle) with horizontal at which B will appear to move as seen from A isView SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
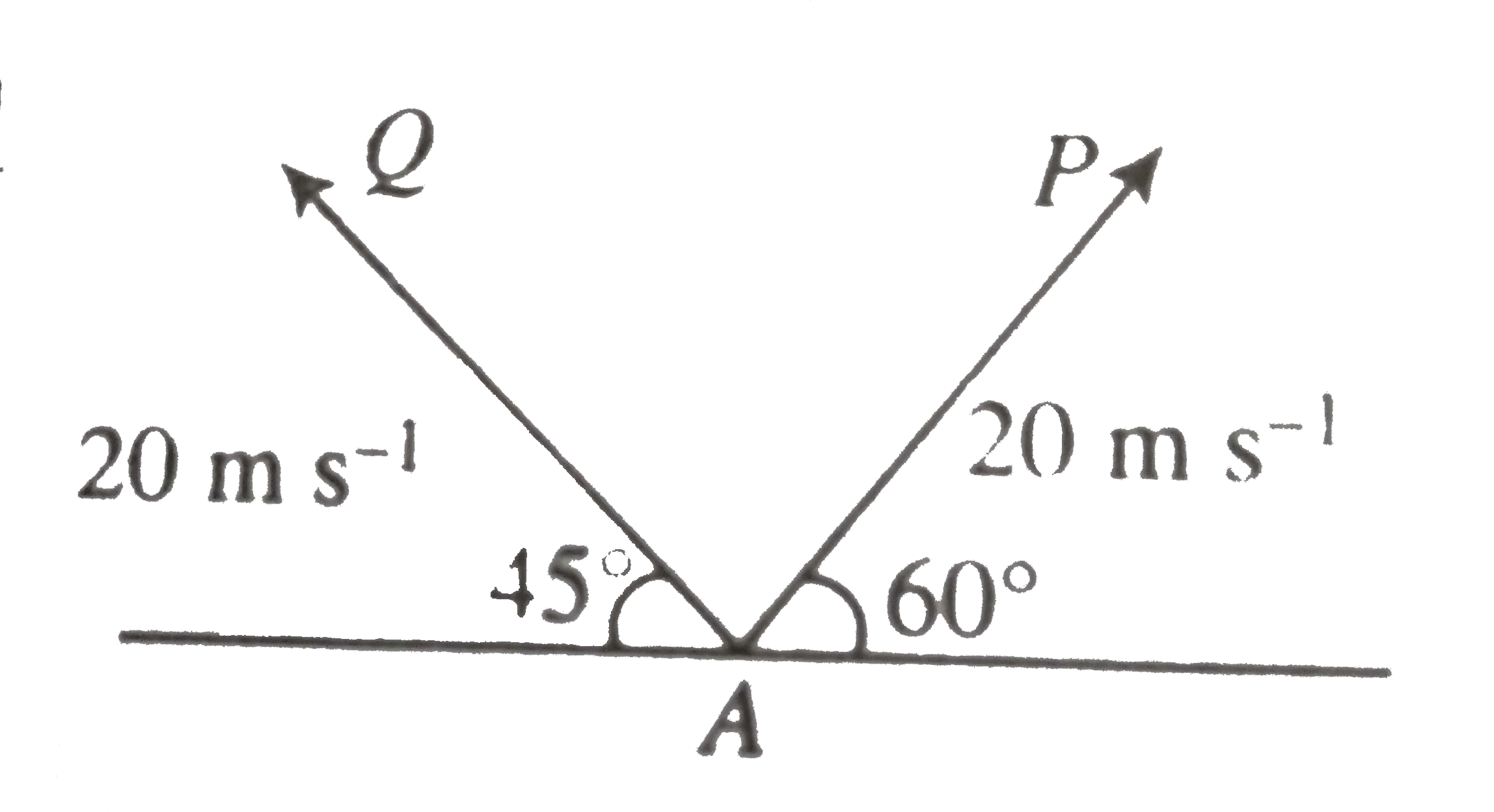 View Solution
View SolutionIn Geiger marsden experiment in a head on collision between an α particles and a gold nucleus the minimum separation is 4×10−14 m . the energy of α particle is
View Solution

