A projectile of mass m is fired frm the surface of the earth at an angle α=60∘ from the vertical. The initial speed v0 is equal to √GMeRe. The maximum height that projectile can rise from the surface of the earth is Rex. Find the value of x?
G= Universal Gravitational constant
Me= mass of earth
Re=Radius of earth

The correct Answer is:2
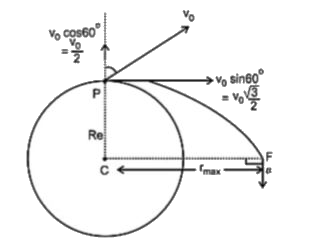
By conservation of angular momentum about C at position P and F
mv0√32Re=mvrmax
⇒v=√3Rev02rmax……i
By conservation of mechanical energy between P and F
12mv20−GMemRe=12mv2−GMemrmax..........ii
Put i and ii
12mv20−GMemRe=12m3R2v204r2maxGMeR−GMemrmax
⇒12Re−1Re=3Rr2max−1rmax
⇒−12Re=3Re−8rmax8r2max
⇒4r2max−8Rermax+3R2e=0
Solving the quadratic in rmax
we get
rmax=8Re±√16Re8=8Re±4Re8
⇒rmax=(8Re)+4Re8=12Re8=3Re2
∴hmax=rmax−Re=3Re2−Re=Re2
∴x=2
Topper's Solved these Questions
Similar Questions
A projectile of mass m is fired from the surface of the earth at an angle α=60∘ from the vertical. The initial speed υ0 is equal to √GMeRe. How high does the projectile rise ? Neglect air resistance and the earth's rotation.
View SolutionA projectile of mass m is fired from the surface of the earth at an angle α=60∘ from the vertical. The initial speed υ0 is equal to √GMeRe. How high does the projectile rise ? Neglect air resistance and the earth's rotation.
View Solution
Knowledge Check
The escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
A√GMeReB√2GMeReC√2GmReDGMeR2eThe escape velocity of a sphere of mass m is given by (G=Universal gravitational constant,M=Mass of the earth and Re=Radius of the earth)
A√2GMmReB√2GMReC√GMReD√2GMm+ReReThe escape velocity from the surface of the earth is (where RE is the radius of the earth )
A√2gREB√gREC2√gRED√3gRE
The escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
View SolutionA projectile is fired from surface of earth at 30∘ above horizontal with speed u=√GMcR where Mc is mass of earth R is radius of earth Find maximum height of the projectile above earth surface
View SolutionA particle is projected vertically upward the surface of the earth (radius Re ) with a speed equal to one-fourth of escape velocity. The maximum height attained by it from the surface of the earth is Rek. Find k.
View SolutionThe escape velocity from the surface of the earth is (where RE is the radius of the earth )
View SolutionA projectile is fired vertically upwards from the surface of the earth with a velocity Kve, where ve is the escape velocity and K<1.If R is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)
View Solution
